Для любых отличных от нуля коллинеарных векторов  и
и  существует такое число λ, что
существует такое число λ, что 
Доказательство
Пусть  и и  одинаково направлены. Векторы одинаково направлены. Векторы  и и  одинаково направлены и имеют одну и ту же абсолютную величину одинаково направлены и имеют одну и ту же абсолютную величину  Значит, они равны: Значит, они равны:   Если векторы Если векторы  и и  противоположно направлены, аналогично заключаем, что противоположно направлены, аналогично заключаем, что   Теорема доказана. Теорема доказана.
|
 Теорема 11.9.
Теорема 11.9.
Пусть  и
и  – отличные от нуля неколлинеарные векторы. Любой вектор
– отличные от нуля неколлинеарные векторы. Любой вектор  можно единственным образом представить в виде
можно единственным образом представить в виде 
Доказательство
Скалярное произведение векторов.
Скалярным произведением векторов  и
и  называется число
называется число  Скалярное произведение векторов
Скалярное произведение векторов  и
и  обозначется
обозначется 
Для любых векторов 
 и
и 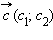 верно:
верно:
· 
· 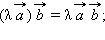
· 
 Теорема 11.10.
Теорема 11.10.
Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
Доказательство
Единичные векторы  и
и  имеющие направления положительных координатных полуосей, называются координатными векторами или ортами.
имеющие направления положительных координатных полуосей, называются координатными векторами или ортами.
 Теорема 11.11.
Теорема 11.11.
Любой ненулевой вектор  единственным образом можно разложить по координатным векторам, то есть записать в виде
единственным образом можно разложить по координатным векторам, то есть записать в виде 
Доказательство
Так как координатные векторы отличны от нуля и неколлинеарны, то любой вектор  допускает разложение по этим векторам в силу теоремы 11.9 допускает разложение по этим векторам в силу теоремы 11.9  Найдем λ и μ. Умножим обе части равенства скалярно на вектор Найдем λ и μ. Умножим обе части равенства скалярно на вектор  Имеем Имеем  С учетом того, что С учетом того, что  и и  ортогональны, имеем ортогональны, имеем  Аналогично, умножая равенство на Аналогично, умножая равенство на  получим получим  или или  Таким образом, для любого вектора Таким образом, для любого вектора  получается разложение получается разложение  Так как в силу теоремы 11.4 и теоремы 11.5 координаты однозначно определяют вектор, то разложение единственно. Теорема доказана. Так как в силу теоремы 11.4 и теоремы 11.5 координаты однозначно определяют вектор, то разложение единственно. Теорема доказана.
|

 и
и  существует такое число λ, что
существует такое число λ, что 
 одинаково направлены и имеют одну и ту же абсолютную величину
одинаково направлены и имеют одну и ту же абсолютную величину  Значит, они равны:
Значит, они равны: 
 Если векторы
Если векторы 
 Теорема доказана.
Теорема доказана.
 Теорема 11.9.
Теорема 11.9. можно единственным образом представить в виде
можно единственным образом представить в виде 
 Проведем через точки A и B прямые, параллельные векторам
Проведем через точки A и B прямые, параллельные векторам  Они пересекутся в некоторой точке C. Имеем
Они пересекутся в некоторой точке C. Имеем  Так как векторы
Так как векторы  коллинеарны, то
коллинеарны, то  так как векторы
так как векторы  и
и 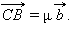 Таким образом,
Таким образом, 
 существуют числа
существуют числа 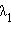 и
и  такие, что
такие, что  и при этом верно хотя бы одно из соотношений
и при этом верно хотя бы одно из соотношений 
 Пусть для определенности
Пусть для определенности  Тогда из равенства
Тогда из равенства  имеем
имеем  На основании теоремы 11.7 и замечания 11.1 получаем, что векторы
На основании теоремы 11.7 и замечания 11.1 получаем, что векторы  и
и  называется число
называется число  Скалярное произведение векторов
Скалярное произведение векторов 

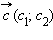 верно:
верно:
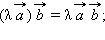



 таким образом, выражается через длины векторов
таким образом, выражается через длины векторов 
 т. е. систему координат можно выбрать любую, а величина скалярного произведения не изменится. Выберем систему координат так, чтобы начало координат совпало с началом вектора
т. е. систему координат можно выбрать любую, а величина скалярного произведения не изменится. Выберем систему координат так, чтобы начало координат совпало с началом вектора  а сам вектор
а сам вектор 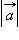 и 0, а вектора
и 0, а вектора  и
и  По определению
По определению

 и
и  имеющие направления положительных координатных полуосей, называются координатными векторами или ортами.
имеющие направления положительных координатных полуосей, называются координатными векторами или ортами.
 Найдем λ и μ. Умножим обе части равенства скалярно на вектор
Найдем λ и μ. Умножим обе части равенства скалярно на вектор  Имеем
Имеем  С учетом того, что
С учетом того, что  и
и  ортогональны, имеем
ортогональны, имеем  Аналогично, умножая равенство на
Аналогично, умножая равенство на  получим
получим  или
или  Таким образом, для любого вектора
Таким образом, для любого вектора 


