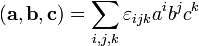Свойства
§ Смешанное произведение кососимметрично по отношению ко всем своим аргументам:
т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что
§ Смешанное произведение
§ Смешанное произведение
В частности, § Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю. § Геометрический смысл — Смешанное произведение
Три вектора, определяющие параллелепипед. § Смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивита:
(в последней формуле в ортонормированном базисе все индексы можно писать нижними; в этом случае эта формула совершенно прямо повторяет формулу с определителем, правда, при этом автоматически получается множитель (-1) для левых базисов).
|
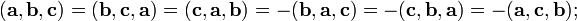
в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов 
и 
:
