Система координат и координаты вектора
Рассмотрим случай трехмерного пространства (на плоскости все построения аналогичны). Фиксируем некоторую точку Если в пространстве выбран базис, то вектор Определение 10.17 Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка Определение 10.18 Координаты радиус-вектора точки Первая координата называется абсциссой, вторая -- ординатой, третья -- аппликатой. Аналогично определяются декартовы координаты на плоскости. Разумеется, точка на плоскости имеет только две координаты -- абсциссу и ординату. Координаты точки обычно пишут в скобках после буквы, обозначающей точку, например Определение 10.19 Декартова система координат называется прямоугольной, если векторы базиса -- единичные и попарно ортогональные (перпендикулярные) друг другу. В дальнейшем мы будем использовать лишь декартову прямоугольную систему координат и для краткости будем называть ее просто "система координат". Единичные попарно ортогональные векторы базиса принято, как правило, обозначать i, j, k. Определение 10.20 Базис, образованный единичными попарно ортогональными векторами, называют ортонормированным. На рис. 10.15 показаны два способа изображения точки
Рис.10.15.Построение точки
Так как точку пространства мы вынуждены изображать на плоскости, то, пока не указаны линии, связывающие изображение точки с осями координат, установить ее положение в пространстве невозможно! Это показывает рис. 10.16.
Рис.10.16.
Зная координаты начала и координаты конца вектора, можно определить координаты самого вектора. Предложение 10.12 Если точки заданы своими координатами Доказательство. Очевидно соотношение
Рис.10.17.Координаты вектора
откуда Преобразование декартовых координат при параллельном сдвиге осей определяется формулами
Здесь x, y - координаты произвольной точки М плоскости относительно старых осей, x’, y’ - координаты той же точки относительно новых осей, a, b - координаты нового начала O’ относительно старых осей (говорят также, что a - величина сдвига в направлении оси абсцисс, b - величина сдвига в направлении оси ординат). Преобразование декартовых прямоугольных координат при повороте осей на угол
Здесь x, y суть координаты произвольной точки М плоскости относительно старых осей, x’, y’ - координаты той же точки относительно новых осей. Формулы
определяют преобразование координат при параллельном сдвиге системы осей на величину а в направлении Ох, на величину b в направлении Оу и последующем повороте осей на угол
|

 и возьмем произвольную точку
и возьмем произвольную точку  . Радиус-вектором точки
. Радиус-вектором точки  .
. ,
,  .
. по ее координатам.
по ее координатам.

 ,
,  , то
, то 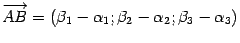 .
. (рис. 10.17),
(рис. 10.17),
 . Так как, по определению, координаты точки совпадают с координатами ее радиус-вектора, то
. Так как, по определению, координаты точки совпадают с координатами ее радиус-вектора, то  ,
, 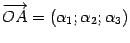 . В силу предложений 10.4, 10.5 получим
. В силу предложений 10.4, 10.5 получим  ,
,  .
. (который надо понимать, как в тригонометрии) определяется формулами
(который надо понимать, как в тригонометрии) определяется формулами ,
,  .
. ,
, 



