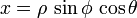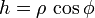Полярные координаты
Полярные координаты. Основная статья: Полярная система координат В полярной системе координат положение точки определяется расстояние до центра координат и углом радиус-вектора с осью Ox. Термин «полярные координаты» используется только на плоскости, в пространстве применяются цилиндрические и сферические системы координат. [править]Цилиндрические координаты
Цилиндрические координаты. Основная статья: Цилиндрическая система координат Цилиндрические координаты — трехмерный аналог полярных, в котором точка P представляется трехкомпонентным кортежем (r,θ, h). В терминах декартовой системы координат, § § § h (высота) — расстояние (с учетом знака) от xy-плоскости до точки P. Примечание: в литературе можно встретить пометку z для h; это не принципиально, но нужно следить, какие отметки применяются. Полярные координаты имеют один недостаток: значение θ теряет смысл, если r = 0. Цилиндрические координаты полезны для изучения систем, симметричных вокруг некой оси. Например, длинный цилиндр в декартовых координатах имеет уравнение 2 x + 2 y = 2 c, тогда как в цилиндрических оно выглядит как r = c [править]Сферические координаты
Сферические координаты. Основная статья: Сферическая система координат Сферические координаты — трехмерный аналог полярных [править]Обозначения, принятые в Америке В сферической системе координат, расположение точки P определяется тремя компонентами: (ρ,ϕ,θ). В терминах декартовой системы координат, § § § Примечание: в литературе можно встретить пометку φ или θ, а также r для ρ; Сферическая система координат также имеет недостаток: φ теряет смысл если ρ = 0, также и θ теряет смысл, если ρ = 0 или φ = 0 или φ = 180°. Для построения точки по её сферическими координатами, нужно: от полюса отложить отрезок, равный ρ вдоль положительной z-оси, вернуть его на угол φ вокруг оси y в направлении положительной x -оси, и вернуть на угол θ вокруг z -оси в направлении положительной y -оси. Сферические координаты полезны при изучении систем, симметричных вокруг точки. Так, уравнение сферы в декартовых координатах выглядит как x 2 + y 2 + z 2 = c 2, тогда как в сферических становится намного проще: ρ = c. [править]Европейские обозначения В Европе принято использовать другие обозначения. Положение точки задаётся числами: (r,θ,φ), Где r — расстояние от точки до начала координат, θ — полярный угол, который изменяется в пределах от 0 до π, [править]Переход из одной системы координат в другую [править]Декартовы и полярные
где u0 — функция Хевисайда с u 0(0) = 0, а sgn — функция signum. Здесь функции u0 и sgn используются как «логические» переключатели, аналогичные по значению операторам «если.. то» (if…else) в языках программирования. Некоторые языки программирования имеют специальную функцию atan2 (y, x), которая находит правильный θ в необходимом квадранте, определённом x и y. [править]Декартовы и цилиндрические
[править]Декартовы и сферические
[править]Цилиндрические и сферические
|
(радиус) — расстояние от оси z к точке P,
(азимут или долгота) — угол между положительной («плюсовой») частью оси x и прямой линии, мысленно проведённой от полюса до точки P, спроектирован на xy-плоскость
(радиус) — это расстояние от точки Р до полюса,
(широта или полярный угол) — угол между z-осью и прямой, проведённой из полюса до точки P
— Азимутальный угол, который изменяется в пределах от 0 до 2π. То есть, в европейской системе, которая применяется также и в России, обозначения для углов переставлены по сравнению с американской.
