Угол между плоскостями
Пусть плоскости Плоскости, пересекаясь, образуют четыре двугранных угла (рис. 11.6): два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой. Мы всегда будем искать острый угол. Для определения его величины возьмем точку
Рис.11.6.Угол между плоскостями
Если через точку
Рис.11.7.Угол между нормальными векторами острый
Рис.11.8.Угол между нормальными векторами тупой
В одном варианте (рис. 11.7) Во втором варианте (рис. 11.8)
то в обоих случаях По определению скалярного произведения
и соответственно
Так как координаты нормальных векторов известны, если заданы уравнения плоскостей, то полученная формула (11.4) позволяет найти косинус острого угла между плоскостями. Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы. Получаем условие перпендикулярности плоскостей:
Если плоскости параллельны, то коллинеарны их нормальные векторы. Получаем условие параллельности плоскостей
где У гол между прямой и плоскостью
Пусть прямая d - не перпендикулярна плоскости θ; d ′− проекция прямой d на плоскость θ; Наименьший из углов между прямыми d и d ′ мы назовем углом между прямой и плоскостью. Обозначим его как φ=(d,θ) Если d ⊥θ, то (d,θ)=π/2
Oi → j → k →− прямоугольная система координат. Уравнение плоскости: θ: Ax + By + Cz + D =0
Вектор n →(A, B, C)⊥θ Тогда остается выяснить угол между векторами n → и p →, обозначим его как γ=(n →, p →). Если угол γ<π/2, то искомый угол φ=π/2−γ. Если угол γ>π/2, то искомый угол φ=γ−π/2 sinφ=sin(2π−γ)=cosγ
sinφ=sin(γ−2π)=−cosγ
sinφ=∣cosγ∣=∣ ∣ Ap 1+ Bp 2+ Cp 3∣ ∣ √ A 2+ B 2+ C 2√ p 21+ p 22+ p 2
|

 и
и  заданы соответственно уравнениями
заданы соответственно уравнениями  и
и  . Требуется найти угол
. Требуется найти угол  между этими плоскостями.
между этими плоскостями. на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры
на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры  и
и  к линии пересечения. Нарисуем также нормальные векторы
к линии пересечения. Нарисуем также нормальные векторы  и
и 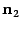 плоскостей
плоскостей 
 , перпендикулярную линии пересечения плоскостей
, перпендикулярную линии пересечения плоскостей 

 и
и  , следовательно, угол
, следовательно, угол  между нормальными векторами равен углу
между нормальными векторами равен углу  , а угол
, а угол  . Так как
. Так как
 .
. . Откуда
. Откуда
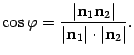


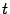 -- любое число.
-- любое число.



