 В багатьох радіотехнічних системах (радіолокаційних, системах багатоканального радіозв’язку) інформація передається з допомогою послідовності прямокутних радіоімпульсів. В таких системах на вході радіоприймачів за звичай ставлять резонансні частотно вибірні системи при проходжені яких, сигнали зазнають деяких спотворень. Для установленя характеру спотворень знайдемо сигнал на виході такої класичної частотно-вибірної системи як послідовний коливальний контур при
В багатьох радіотехнічних системах (радіолокаційних, системах багатоканального радіозв’язку) інформація передається з допомогою послідовності прямокутних радіоімпульсів. В таких системах на вході радіоприймачів за звичай ставлять резонансні частотно вибірні системи при проходжені яких, сигнали зазнають деяких спотворень. Для установленя характеру спотворень знайдемо сигнал на виході такої класичної частотно-вибірної системи як послідовний коливальний контур при  . Скористаємося операторним методом. Операторна схема заміщення при нульових початкових умовах показана на рис. Зображення напруги на конденсаторі очевидно дорівнює:
. Скористаємося операторним методом. Операторна схема заміщення при нульових початкових умовах показана на рис. Зображення напруги на конденсаторі очевидно дорівнює:
 ,
,
де:  - резонансна частота послідовного коливального контуру;
- резонансна частота послідовного коливального контуру;  .- декремент затухання.
.- декремент затухання.
Для знаходження оригіналу скористаємося формулами розкладання (першою формулою Хевісайда). Нехай параметри елементів контура відповідають коливальному режиму. Тоді многочлен у знаменнику має чотири корені:  ,
,  ,
,  ,
,  . Тут
. Тут  - частота власних коливань контуру.
- частота власних коливань контуру.
Отже
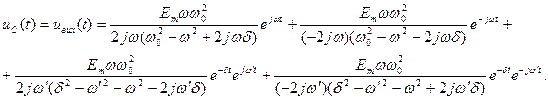
Якщо частота впливу співпадає з резонансною частотою контуру ( ), а контур високодобротний (
), а контур високодобротний ( ), то
), то
 .
.
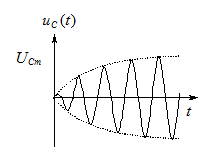
 Характер зміни напруги на конденсаторі високодобротного контуру при збуджені на резонансній частоті має вигляд гармонічного коливання у якого амплітуда промодульована експонентою. З часом, напруга на виході наближається до усталеного, стаціонарного значення (рис). При цьому, при незначних декрементах затухання, амплітуда стає ’’фантастичною’’, проте її установлення триває досить довго. Іншими словами - явище резонансу, характерне для усталеного режиму, довго не наступає.
Характер зміни напруги на конденсаторі високодобротного контуру при збуджені на резонансній частоті має вигляд гармонічного коливання у якого амплітуда промодульована експонентою. З часом, напруга на виході наближається до усталеного, стаціонарного значення (рис). При цьому, при незначних декрементах затухання, амплітуда стає ’’фантастичною’’, проте її установлення триває досить довго. Іншими словами - явище резонансу, характерне для усталеного режиму, довго не наступає.
На частотах збудження  , що відрізняються в незначній мірі від резонансної частоти контуру та незначних затуханнях (
, що відрізняються в незначній мірі від резонансної частоти контуру та незначних затуханнях ( ), на початковій стадії перехідних процесів (
), на початковій стадії перехідних процесів ( ) формула () трансформується у наступну
) формула () трансформується у наступну
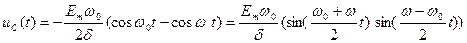 .
.
По своєму характеру це амплітудно модульовані коливання з частотою модуляції  значно меншою від частоти джерела
значно меншою від частоти джерела  (рис). Такий характер модульованих коливань відомий під назвою биття.
(рис). Такий характер модульованих коливань відомий під назвою биття.
Основные уравнения гидродинамики
План:
1. Уравнение неразрывности для элементарной струйки и потока жидкости
2. Уравнение Бернулли для элементарной струйки
3. Уравнение Бернулли для потока реальной жидкости
4. Уравнение равномерного движения

 В багатьох радіотехнічних системах (радіолокаційних, системах багатоканального радіозв’язку) інформація передається з допомогою послідовності прямокутних радіоімпульсів. В таких системах на вході радіоприймачів за звичай ставлять резонансні частотно вибірні системи при проходжені яких, сигнали зазнають деяких спотворень. Для установленя характеру спотворень знайдемо сигнал на виході такої класичної частотно-вибірної системи як послідовний коливальний контур при
В багатьох радіотехнічних системах (радіолокаційних, системах багатоканального радіозв’язку) інформація передається з допомогою послідовності прямокутних радіоімпульсів. В таких системах на вході радіоприймачів за звичай ставлять резонансні частотно вибірні системи при проходжені яких, сигнали зазнають деяких спотворень. Для установленя характеру спотворень знайдемо сигнал на виході такої класичної частотно-вибірної системи як послідовний коливальний контур при  . Скористаємося операторним методом. Операторна схема заміщення при нульових початкових умовах показана на рис. Зображення напруги на конденсаторі очевидно дорівнює:
. Скористаємося операторним методом. Операторна схема заміщення при нульових початкових умовах показана на рис. Зображення напруги на конденсаторі очевидно дорівнює: ,
, - резонансна частота послідовного коливального контуру;
- резонансна частота послідовного коливального контуру;  .- декремент затухання.
.- декремент затухання. ,
,  ,
,  ,
,  . Тут
. Тут  - частота власних коливань контуру.
- частота власних коливань контуру.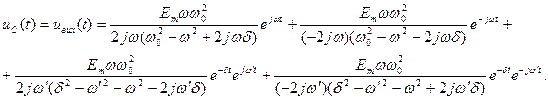
 ), а контур високодобротний (
), а контур високодобротний ( ), то
), то .
.
 Характер зміни напруги на конденсаторі високодобротного контуру при збуджені на резонансній частоті має вигляд гармонічного коливання у якого амплітуда промодульована експонентою. З часом, напруга на виході наближається до усталеного, стаціонарного значення (рис). При цьому, при незначних декрементах затухання, амплітуда стає ’’фантастичною’’, проте її установлення триває досить довго. Іншими словами - явище резонансу, характерне для усталеного режиму, довго не наступає.
Характер зміни напруги на конденсаторі високодобротного контуру при збуджені на резонансній частоті має вигляд гармонічного коливання у якого амплітуда промодульована експонентою. З часом, напруга на виході наближається до усталеного, стаціонарного значення (рис). При цьому, при незначних декрементах затухання, амплітуда стає ’’фантастичною’’, проте її установлення триває досить довго. Іншими словами - явище резонансу, характерне для усталеного режиму, довго не наступає. , що відрізняються в незначній мірі від резонансної частоти контуру та незначних затуханнях (
, що відрізняються в незначній мірі від резонансної частоти контуру та незначних затуханнях ( ), на початковій стадії перехідних процесів (
), на початковій стадії перехідних процесів ( ) формула () трансформується у наступну
) формула () трансформується у наступну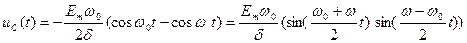 .
. значно меншою від частоти джерела
значно меншою від частоти джерела 


