Уравнение Бернулли для элементарной струйки идеальной жидкости. Уравнения динамического равновесия жидкости (уравнения Эйлера) можно получить из уравнений равновесия покоящейся жидкости
Уравнения динамического равновесия жидкости (уравнения Эйлера) можно получить из уравнений равновесия покоящейся жидкости, если в них, по закону Д'Аламбера, ввести составляющие силы инерции по соответствующим осям
для частицы жидкости с массой m = 1,
а для двух сечений элементарной струйки идеальной жидкости Получили уравнение Бернулли для элементарной струйки идеальной жидкости, где сумма 3-х величин называется гидродинамическим напором (Hd). Каждый член уравнения Бернулли представляет собой удельную энергию элементарной струйки в каком-либо сечении по отношению к плоскости сравнения. Эта энергия состоит из 3-х частей: 1) удельная энергия положения, измеряемая координатой z над плоскостью сравнения; 2) удельная энергия абсолютного давления, мерой которой служит абсолютная пьезометрическая высота 3) удельная кинетическая энергия, мерой которой является скоростной напор При этом Рассмотрим реальную жидкость, она характеризуется наличием сил трения, которые возникают при ее движении. Обозначим hf– мера механической энергии, теряемой единицей веса жидкости при перемещении ее вдоль струйки от сечения 1 до сечения 2, назовем ее потери напора. Тогда для элементарной струйки реальной жидкости
|

 ;
; ;
;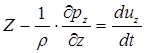 ;
; ;
;
 ;
; – полный дифференциал потенциальной энергии массовых сил;
– полный дифференциал потенциальной энергии массовых сил; – полный дифференциал гидродинамического давления;
– полный дифференциал гидродинамического давления; – полный дифференциал половины квадрата скорости.
– полный дифференциал половины квадрата скорости.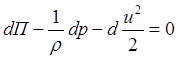 ,
,
 ; члены уравнения разделим на (–g);
; члены уравнения разделим на (–g);  ;
; , интегрируя это выражение, получим
, интегрируя это выражение, получим ,
, .
. ;
; .
. – удельная потенциальная энергия струйки по отношению к плоскости сравнения;
– удельная потенциальная энергия струйки по отношению к плоскости сравнения;  .
.


