Идеальный газ в недеформируемом пласте
Найдём распределение давления в круговом пласте и выведем формулу притока газа к скважине. С этой целью выразим скорость через приведённый объёмный расход
Подставим выражение (3.49) в (3.46) и заменив плотность по уравнению состояния (2.29) получим
Разделив переменные и проинтегрировав в пределах р - рс и r - rc имеем
Распределение давления по (3.51) отличается от распределения давления по закону Дарси наличием последнего члена, что диктует более резкое изменение давления в призабойной зоне. Интегрируя уравнение(3.50) в пределах рк - рс и Rк - rc получим выражение для притока при пренебрежении 1/Rк по сравнении с 1 / rc
или в общепринятом виде
Коэффициенты А и В определяют по данным исследования скважин при установившихся режимах.
Для трещиноватой среды двухчленный закон записывается в виде
где Умножим все члены (1.46) на плотность r и вынесем за скобки вязкость h. Тогда применительно к плоско-радиальному потоку получим:
где После разделения переменных и интегрирования (3.54) в пределах rc - rк; jс - jк получим
Если в (3.56) подставим выражение для трещинной проницаемости и выразим массовый дебит через объёмный, то будем иметь окончательное выражение
Как видно из (3.57), индикаторная кривая в этом случае определяется в результате сложения двух парабол - параболы четвёртого порядка, симметричной относительно оси, параллельной оси дебитов, и параболы второго порядка (относительно дебита Q) симметричной относительно оси, параллельной оси депрессий (Dрс) и отстоящей от последней на расстоянии, равном
Из (3.56) при подстановке выражений для плотности, проницаемости и приведённого к стандартным условиям объёмного дебита можно получить следующее выражение
|

 . 3.49
. 3.49 . 3.50
. 3.50 . 3.51
. 3.51 . 3.52
. 3.52 . 3.53
. 3.53 3.2.5.3. Однородная несжимаемая жидкость в деформируемом (трещиноватом) пласте
3.2.5.3. Однородная несжимаемая жидкость в деформируемом (трещиноватом) пласте , 1.46
, 1.46 ; lбл - средний линейный размер блока.
; lбл - средний линейный размер блока. , 3.54
, 3.54 .
. , 3.56
, 3.56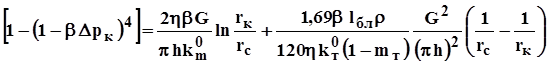 3.57
3.57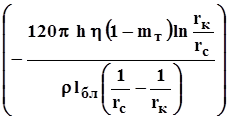 .
.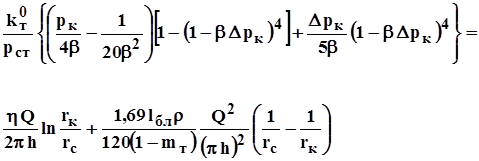 . 3.58
. 3.58


