Предельные теоремы для биномиального распределения
При Распределение Пуассона (закон редких явлений)
Случайная величина
Пример распределения Пуассона. На плоскость (на прямую, в пространство) случайно бросают точки со средней плотностью а точек на единицу площади. Если: 1) вероятность попадания т точек в некоторую фиксированную область D площадью 2) в непересекающиеся области точки попадают независимо друг от друга; 3) вероятность попадания в область малой площади двух и более точек много меньше вероятности попадания одной точки, то распределение точек описывается распределением Пуассона: P (попадание в D m точек) =
Использование примера:радиоактивный распад, булочки с изюмом, разброс осколков снаряда, заболевание редкими (не инфекционными) болезнями, заградительный зенитный огонь, очаги пожаров в городе.
M ξ = D ξ = λ => λ - безразмерная величина!
Биномиальное распределение при р ≈ 0, np < 10 хорошо приближается распределением Пуассона с λ = np.
График
ДЗ.: Исследовать дискретное равномерное распределение.
Равномерное распределение ξ на [ a, b ] Определяется ПР
которых x f(x) >1 ФР ξ
График
При
Пусть η=kξ+l. Тогда η; имеет равномерное распределение на [ka+l, kb+l] при k>0 и на [kb+l, ka+l] при k<0. Почему не существует равномерное распределение ξ на Примеры равномерных распределений:
|


 имеет распределение Пуассона, если
имеет распределение Пуассона, если - параметр распределения. Доказано, что M ξ= D ξ =λ.
- параметр распределения. Доказано, что M ξ= D ξ =λ. зависит только от величины
зависит только от величины  где λ =
где λ =  при λ = 3. (см. таблицу)
при λ = 3. (см. таблицу)
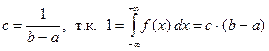 Важный пример: при b-a =0,5
Важный пример: при b-a =0,5 c =2, т.е. возможно, для не-
c =2, т.е. возможно, для не-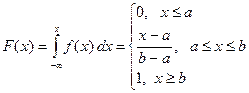

 - зависит только от длины [α, β] и не зависит от расположения [α, β] в [ a, b ].
- зависит только от длины [α, β] и не зависит от расположения [α, β] в [ a, b ].

 - бесконечное множество – любое значение из [ a, b ].
- бесконечное множество – любое значение из [ a, b ]. ?
?


