Биномиальное распределение
Мода Для дискретной ξ мода
(*) Асимметрия и эксцесс случайной величины ξ;
Насколько распределение случайной величины ξ близко к нормальному? ПР ξ ~ N (μ, σ) симметрична относительно х = μ.
] ξ – произвольная,
Для нормального распределения ξ А ξ = 0.
Графики Для произвольной ξ с ПР f (x) и M ξ = μ
График
Для биномиального распределения
Начальные
ОСНОВНЫЕ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН И ИХ ХАРАКТЕРИСТИКИ Биномиальное распределение
Пример. ξ - число наступления события А в испытаниях Бернулли.
Определение. Случайная величина ξ имеет биномиальное распределение, если:
0 < p < 1 - параметр биномиального распределения, в испытаниях Бернулли – вероятность наступления А в одном опыте. q = 1 – p
Покажем, что M ξ = np, D ξ = npq. Действительно, рассмотрим один опыт, в котором случайная величина η принимает значение 1 с вероятностью р и 0 с вероятностью q = 1 – p.
n раз, незав.(не важно для M ξ, важно для Dξ;!) D ξ = npq. Действительно,
При p = q = ½
При произвольном
и находится из него.
|
График
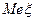- любая точка из 
.
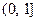. Для непрерывной ξ с плотностью распределения f (x) 
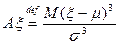- асимметрия ξ.
- эксцесс ξ, даёт оценку “остроты” ПР ξ по сравнению с ПР N (μ, σ)
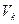и центральные 
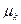моменты k – го порядка случайной величины ξ: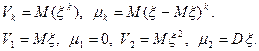
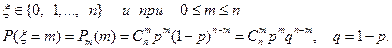
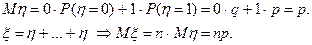
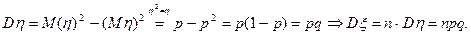
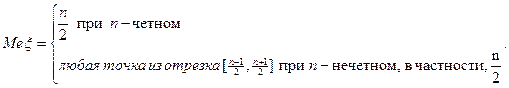
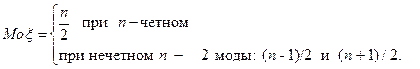
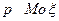удовлетворяет неравенству
