Пусть случайные величины  независимы и имеют одинаковое распределение с математическим ожиданием μ<∞ и дисперсией
независимы и имеют одинаковое распределение с математическим ожиданием μ<∞ и дисперсией  Тогда
Тогда
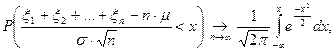 или
или
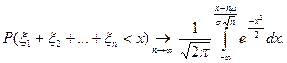
Таким образом, распределение суммы 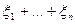 таких случайных величин при n → ∞ стремится к нормальному распределению.
таких случайных величин при n → ∞ стремится к нормальному распределению.
Важность этой теоремы, которая остается справедливой и при меньших ограничениях на случайные величины  , состоит в том, что в большинстве исследований некоторой случайной величины
, состоит в том, что в большинстве исследований некоторой случайной величины  априорно неизвестен закон ее распределения. Но, если случайная величина
априорно неизвестен закон ее распределения. Но, если случайная величина  формируется под воздействием многих случайных факторов (случайных величин)
формируется под воздействием многих случайных факторов (случайных величин)  , которые могут быть даже слабо связаны между собой, но ни один из них не превалирует над остальными, то можно ожидать, что
, которые могут быть даже слабо связаны между собой, но ни один из них не превалирует над остальными, то можно ожидать, что  будет иметь, хотя бы и приближенно, нормальное распределение, параметры которого оцениваются методами математической статистики.
будет иметь, хотя бы и приближенно, нормальное распределение, параметры которого оцениваются методами математической статистики.