Закон больших чисел. Формулировка Чебышева
Пусть случайные величины
Из этой сложной и малопонятной для нас теоремы следует
Теорема 1 (Об устойчивости средних).Пусть Тогда для любого
Проиллюстрируем смысл этой теоремы на примере. Пусть требуется возможно более точно измерить вес некоторого тела с помощью весов, не имеющих систематической ошибки. Результат одного взвешивания этого тела (одного опыта) – значение случайной величины ξ;. Так как при взвешивании отсутствует систематическая ошибка, можно предположить, что истинный вес μ; этого тела равен математическому ожиданию случайной величины ξ: μ=Мξ;. Проведем n взвешиваний и возьмем среднее арифметическое (ξ1+ ξ2+…+ξn)/n их результатов ξ1, ξ2,…, ξn. Согласно теореме 1 при возрастании n это среднее арифметическое приближается (весьма сложным образом) к μ; – истинному весу тела. Таким образом, теорема 1 даем теоретическое обоснование широко используемому методу повышения точности измерений – надо провести несколько измерений и взять среднее арифметическое их результатов.
Теорема 2 (Теорема Бернулли). Пусть m - число наступления события А в n испытаниях Бернулли, p = P (A) - вероятность А в одном испытании. Тогда для любого
Значение этой теоремы невозможно переоценить. Во-первых, теорема дала содержательную интерпретацию формально введенного понятия вероятности Р(А) некоторого события А – Р(А) показывает, насколько часто в серии опытов можно ожидать наступления события А. Во-вторых, вероятность Р(А) некоторого события А, которую, как правило, невозможно найти математически, можно оценить, хотя бы и приближенно, с помощью относительной частоты наступления события А в серии опытов.
|

 попарно независимы и
попарно независимы и  Тогда для любого
Тогда для любого 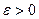
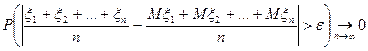
 попарно независимы,
попарно независимы,  и
и 

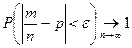 или
или  - относительная частота наступления события А в серии из n опытов.
- относительная частота наступления события А в серии из n опытов.


