Нормальное распределение
Случайная величина ξ распределена по нормальному закону с параметрами μ и σ>0
Смысл параметров:
|| Me ξ = Mo ξ
Вероятность попадания ξ в заданный интервал (a, b) ФР нормального распределения ξ ~ N (μ, σ)
интеграл вероятностей Смысл замены
Центрированная случайная величина – математическое ожидание равно нулю. Нормированная случайная величина – дисперсия равна единице.
Интеграл вероятностей (*) не выражается через элементарные функции. Для вычисления (*) используются таблицы функции Лапласа
Функция Лапласа нечетная: Ф (- x) = - Ф (x), поэтому её таблицы составлены только при x > 0. Из (*) следует
и Ф(-x)= -Ф(x). Через ФР легко находится
по таблице Ф (x)
Частный случай: при
При k = 3 - «правило трех сигм»:
график Если ξ~N(μ, σ) и η=k·ξ+l, то η~N(μ+l, |k|·σ).
|
если её ПР равна
график – «гауссов» колокол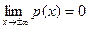
(*)
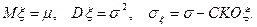
- переход от случайной величины ξ ~ N (μ, σ) к центрированной и нормированной (стандартизованной) случайной величине 
, 
, т.к. 
.
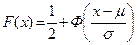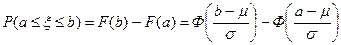
Таким образом, ФР случайной величины ξ ~ N (μ, σ) выражается через функцию Лапласа формулой
(**)
и
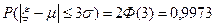- ограниченность (локализация ξ) энергии процесса
- точки перегиба p (x) –плотности нормального распределения.
