Федеральное агентство по образованию
Министерство образования и науки Российской Федерации
СБОРНИК ЗАДАЧ учебной дисциплины «Управленческие решения»
СОДЕРЖАНИЕ ЗАДАЧА 1 «Принятие решения о целесообразности экспорта»................ 4 ЗАДАЧА 2 «Принятие решения по маркетингу»........................................ 6 ЗАДАЧА 3 «Принятие решения по политике цен»...................................... 7 ЗАДАЧА 4 «Выбор решения по количественной шкале оценок прибыли и известной вероятности проявления ситуаций»...................................................... 9 ЗАДАЧА 5 «Выбор решения по качественной шкале оценок эффективности и известной вероятности проявления ситуаций».................................................... 10 ЗАДАЧА 6 «Выбор решения по количественной шкале оценок затрат и переменной вероятности проявления ситуаций»................................................ 13 ЗАДАЧА 7 «Построение дерева решений при определении продуктовой стратегии фирмы и стратегии развития ее производственных мощностей»...... 15 ЗАДАЧА 8 «Выбор решения в условиях неопределенности и количественной шкалы оценок»...................................................................................................... 18 ЗАДАЧА 9 «Определение эффективных решений»................................... 20 ЗАДАЧА 10 «Оценка согласованности мнений экспертов»...................... 21 ЗАДАЧА 11 «Групповая оценка объектов»............................................... 25 ЗАДАЧА 12................................................................................................. 27 ЗАДАЧА 13................................................................................................. 28 ЗАДАЧА 14................................................................................................. 29 ЗАДАЧА 15................................................................................................. 29 ЗАДАЧА 16................................................................................................. 31 ЗАДАЧА 17................................................................................................. 33 ЗАДАЧА 18................................................................................................. 35 ЗАДАЧА 19................................................................................................. 36 ЗАДАЧА 20................................................................................................. 37 ЗАДАЧА 1 «Принятие решения о целесообразности экспорта» Условие. Фирма «Альфа» производит некоторую продукцию промышленности строительных материалов и обычно продает ее оптовикам на внутреннем рынке по цене Ц1 ден. ед., за единицу продукции (здесь и далее цифры измерения носят условный характер). Мощность фирмы – М единиц продукции в месяц. В настоящее время ее месячный выпуск составляет О1 единиц. Имеется N-кратный запас мощности (М = О1* N) Фирме было предложено заключить контракт на экспорт О2 единиц продукции ежемесячно по цене Ц2 ден. ед. Базис поставки – «самовывоз», без обязательства по транспортировке товара на продавце. Издержки на производство и сбыт в расчете на единицу продукции приведены в табл. 1.1. Таблица 1.1 - Издержки на производство и сбыт единицы продукции
Управляющий фирмой не пожелал заключить контракт в связи с тем, что предлагаемая цена Ц2 не покрывает издержек С за единицу продукции. Требуется определить: 1) правильное ли решение принял управляющий, и как изменилась бы прибыль фирмы, если бы он принял предложение зарубежного партнера? 2) как изменилась бы прибыль фирмы, если бы предложение было принято, но запас мощности фирмы составлял бы N = 1)? Методические рекомендации по решению: В данной задаче необходимо выбрать решение из альтернативы «принимать или не принимать предложение зарубежной фирмы?» для двух условий: 1) имеется N-кратный запас мощности (например, N = 2); 2) мощности фирмы «Альфа» полностью загружены (N = 1). 1. В текущий момент прибыль составляет: П1 = (Ц1 – С1) * О1 = (20 – 18) * 1000 = 2000 ден. ед. в месяц где П1 – текущая прибыль; Ц1 – цена продукции при продаже на внутреннем рынке; C1 – издержки на единицу продукции из продаваемой партии С1 = Х1 + Х2 + Х3 + Х4 + Х5; О1 – текущий объем продаж в месяц. Если бы управляющий принял предложение, то себестоимость единицы продукции экспортной партии составила бы всего С2 = Х1 + Х2 + Х3 = 2 + 7 + 2 = 11 ден. ед., поскольку постоянные накладные уже отнесены к «внутренней» партии и условия самовывоза не требуют издержек по сбыту. В этих условиях дополнительная прибыль составила бы: П2 = (Ц2 – С2) * О2 = (15 – 11) * 500 = 2000 ден. ед. в месяц Индекс «2» отнесен к показателям экспортной партии. Таким образом, общая прибыль удвоилась бы и составила П = П1 + П2 = 4000 ден. ед. в месяц. Следовательно, управляющий принял неверное решение. К тому же выводу можно прийти, если несколько модифицировать расчет в сторону большей корректности рассуждений, пересчитав суммы постоянных накладных на единицу продукции при повышении выпуска в 1,5 раза. В этом случае постоянные накладные на единицу продукции составят Х41 = Х4/1,5 = 5/1,5 = 3,33 ден. ед. и, следовательно, издержки по продукции на внутреннем рынке будут равны С11 = Х1 + Х2 + Х3 + Х41 + Х5 = 2 + 7 + 2 + 3,33 + 2 = 16,33 ден. ед., а экспортной продукции – С21 = Х1 + Х2 + Х3 + Х41 = 2 + 7 + 2 + 3,33 = 14,33 ден. ед. Общая прибыль при этом составит: П = П1 + П2 = (Ц1 – С11) * О1 + (Ц2 – С21) * О2 = = (20 – 16,33) * 1000 + (15 – 14,33) * 500 = 3670 + 330 = 4000 ден. ед. 2. Во втором случае экспорт продукции должен осуществляться за счет сокращения объема продаж на внутреннем рынке. Постоянные накладные на единицу продукции при этом не меняются. Общие издержки на единицу продукции для внутренних продаж сохраняются на уровне С1 = 18 ден. ед., а для экспортной продукции составят С2 = 16 ден. ед. (с учетом «самовывоза»). Общая прибыль при этом будет равна: П = П1 + П2 = (Ц1 – С1) * (О1 – О2) + (Ц2 – С2) * О2 = = (20 – 18) * 500 + (15 – 16) * 500 = 500 ден. ед., т.е. при загруженных мощностях данное предложение об экспорте было бы невыгодным, поскольку прибыль упала бы в 4 раза.
ЗАДАЧА 2 «Принятие решения по маркетингу» Условие. Руководителю предприятия представлен анализ нового продукта марки А. Он решил, что продукт А будет продаваться по розничной цене Ц ден.ед. (по его исследованиям рынка). Розничные торговцы предполагают колебание цен в пределах Рр от продажной цены, а оптовые Ро. Переменные издержки на единицу продукта должны составить Ипер ден. ед., а предполагаемые постоянные на выпуск всей партии Ипост. Требуется принять решение о целесообразности производства нового продукта при ожидаемом объеме продаж в О единиц. Методические рекомендации по решению. Приведем вероятностную задачу к детерминированному виду, установив минимальное значение продажной цены с учетом мнений продавцов согласно самой пессимистической оценке. Такую оценку дали розничные торговцы (Рр = 40%). Поэтому минимальная цена колеблется на уровне Рмин = (100 – Рр)/100 = (100 – 40)/100 = 0,6 от прогнозной: Цмин = Рмин * Ц = 0,6 * 10 = 6 ден. ед. Затем, суммируя постоянные (И1пост) и переменные (Ипер) издержки на единицу продукции, определяем себестоимость (С); при этом постоянные издержки рассчитываются исходя из общей суммы и объема выпуска: И1пост = Ипост / О = 28000/9000 = 3,1 ден. ед. С = Ипер + И1пост = 2 + 3,1 = 5,1 ден. ед. Сравнивая себестоимость с ценой, можно сделать выбор решения из альтернативы «да – нет»: поскольку себестоимость производства (С = 5,1 ден. ед.) меньше продажной цены, определенной по самой пессимистической оценке (Цмин = 6 ден.ед.), то производство продукции марки А является целесообразным. ЗАДАЧА 3 «Принятие решения по политике цен» Условие. Пусть производится некоторый товар А. Исходные данные приведены в табл. 3.1. Таблица 3.1 - Издержки на производство и сбыт продукции А
Требуется определить: 1) сколько продукции (Ог) надо продать, чтобы сделать задуманное предприятие самоокупаемым? 2) сколько продукции надо продать, чтобы получить Птр = 1000 ден.ед. прибыли? 3) какое решение будет лучшим при установлении цены, если известно, что продавая продукцию по цене Ц1 за единицу, можно прогнозировать уровень продаж в О1 единиц продукции в месяц, а по цене Ц2 уровень продаж составит О2 единиц продукции в месяц? Методические рекомендации по решению: 1. Определим прибыль предприятия как разность между суммой, вырученной от продаж, и затратами (переменными и постоянными) на производство: П = Ц * Ог – Ипер * Oг – Ипост, (3.1) где П – прибыль за год; Ц – цена за единицу; Oг – годовой объем производства; Ипост = Иа + Изп + Ир. Для самоокупаемости (безубыточности) необходимо, чтобы П была больше или равна нулю. Отсюда Ц * Ог – Ипер * Ог – Ипост ³ 0 или Ог * (Ц – Ипер) ³ Ипост,. (3.2) Следовательно, минимальный объем выпуска находится из условия: Ог ³ Ипост / (Ц – Ипер). (3.3) Подставляя значения параметров (Ипост = 5000 + 10000 + 2000 = 17000; Ц = 1,5; Ипер = 0,75), получаем: Ог ³ 17000 / (1,5 – 0,75) = 17000 / 0,75 = 22667; Ог ³ 22667 единиц продукции в год (или ³ 1889 единиц в месяц). 2. Для определения объема выпуска, при котором достигается заданный уровень прибыли (Птр = 1000 ден.ед.), используется формула 3.1. Преобразованная к виду 3.2а и 3.3а она дает следующий результат: Ц * Ог – Ипер * Ипост ³ П или Ог * (Ц – Ипер) ³ Ипост + П, (3.2а) Ог ³ (Ипост + П) / (Ц – Ипер). (3.3а) Подставляя значения параметров, получаем: Ог ³ (17000 + 1000) / (1,5 – 0,75) = 18000 / 0,75 = 24000; Ог ³ 24000 единиц продукции в год (или ³ 2000 единиц в месяц). 3. Подставим в формулу 3.1 прогнозные значения объемов продаж для двух вариантов цены (приведя объемы к годовым) и проведем расчеты: П1 = (1,5 – 0,75) * 1500 * 12 – 17000 = 13500 – 17000 = - 3500; П2 = (3 – 0,75) * 500 * 12 – 17000 = 13500 – 17000 = - 3500. Вывод: оба варианта являются равноубыточными, т.е. при таких условиях выпуск продукции А является нецелесообразным.
ЗАДАЧА 4 «Выбор решения по количественной шкале оценок прибыли и известной вероятности проявления ситуаций» Условие. Имеются допустимые решения Yi при четырех возможных ситуациях Sj. Известна вероятность проявления ситуаций - Pj. Платежная матрица
Предпочтения решения для каждой ситуации, определенные индивидуальным ЛПР по количественной шкале в условных единицах, приведены в табл. 4.1 Таблица 4.1 - Платежная матрица с известной вероятностью событий
Требуется определить оптимальное по критерию среднего выигрыша (Байеса-Лапласа) решение Y*. Методические рекомендации по решению. Поскольку коэффициенты матрицы в данном случае отражают поступления на фирму, то пользуясь стандартной формулой для расчета коэффициентов важности решения
определим коэффициенты bi: b1 = 0,1 * 1 + 0,2 * 4 + 0,5 * 5 + 0,2 * 9 = 5,2; b2 = 0,1 * 3 + 0,2 * 8 + 0,5 * 4 + 0,2 * 3 = 4,5; b3 = 0,1 * 4 + 0.2 * 6 + 0,5 * 6 + 0,2 * 2 = 5,0 и занесем их в последнюю графу табл. 4.2. По формуле 4.1 выберем оптимальное решение, которое соответствует максимальному значению коэффициента bi = 5,2, т.е. Y* = Y1. Примечание. Если бы элементы матрицы отражали затраты (о чем было бы указано в условии), то расчет коэффициентов остался тем же, а решение выбиралось бы исходя из минимума средних затрат. ЗАДАЧА 5 «Выбор решения по качественной шкале оценок эффективности и известной вероятности проявления ситуаций» Условие. Имеются три допустимые решения при трех возможных ситуациях. Известна вероятность проявления ситуаций.
Порядковые предпочтения для каждой ситуации, определенные индивидуальным ЛПР по качественной шкале, приведены в табл. 5.1.
Таблица 5.1 - Ранговые предпочтения решений для разных ситуаций и известной вероятности их возникновения
Требуется определить оптимальное по критерию среднего выигрыша решение Y*. Методические рекомендации по решению. Используя формулу
0 при fi,j > fk,j построим три (по количеству ситуаций) квадратные матрицы парных сравнений размерностью, определяемой количеством альтернативных решений (m = 3). Первая матрица для j = 1 строится следующим образом. Первый столбец строится для k = 1 путем последовательного сравнения элемента f1,1 с элементами fi,1 где i = Таблица 5.2,а Таблица 5.2,б Таблица 5.2, в
Элементы итоговой матрицы ||Yi,k|| рассчитываются в два этапа по следующим формулам.
0 при
На первом этапе производится расчет суммы Таблица 5.3 - Последовательность расчета итоговой матрицы ||Yi,k||
Итоговая матрица ||Yi,k|| приведена в табл. 5.4. Расчет коэффициентов bi производится по формуле 5.3 (см. две последние графы в табл. 5.4 и итоговую строку).
Таблица 5.4 - Итоговая матрица ||Yi,k||
Наибольшее значение b1 = 0,5 соответствует 1-му варианту решения, поэтому согласно формуле 4.1 Y* = Y1. ЗАДАЧА 6 «Выбор решения по количественной шкале оценок затрат и переменной вероятности проявления ситуаций» Условие. СМУ заказывает дневную норму раствора бетона у зaвoда ЖБИ на сумму П1 условных единиц. В случае отсутствия поставки СМУ несет ущерб в размере П2 ден. ед. от простоя рабочих. Вероятность поставки составляет Р1. Для того чтобы повысить вероятность поставки, СМУ может а) послать свой транспорт; дополнительные расходы составят П3 ден.ед.; вероятность поставки возрастет до Р2; б) послать представителя на завод ЖБИ и свой транспорт; дополнительные расходы на командирование составят П4 ден. ед., плюс расходы на транспорт П3 ден. ед.; вероятность поставки возрастает до Р3; в) заказать дневную норму у другого поставщика по цене П5 (выше, чем у завода ЖБИ) на условиях самовывоза; вероятность поставки дополнительного заказа составляет Р4; при этом с вероятностью Р1 существует опасность двойной поставки, которая потребует дополнительные затраты на оплату сверхурочных в сумме П6 ден. ед. Следует иметь в виду, что СМУ не хочет разрывать договорные отношения с заводом ЖБИ, поскольку завод является основным поставщиком строительных конструкций. Наименования переменных приведены в табл. 6.1. Таблица 6.1 - Исходные данные к задаче
Требуется определить оптимальные действия СМУ, обеспечивающие минимум потерь. Методические рекомендации по решению. Обозначим Yi управленческие решения СМУ: Y1 – оставить как есть; Y2 – послать свой транспорт; Y3 – послать представителя и транспорт; Y4 – сделать дополнительный страховочный заказ. Ситуации Sj определяются поведением основного поставщика – завода ЖБИ: S1 – поставка есть; S2 – поставки нет. Оценим затраты при разных управленческих решениях в различных ситуациях (см. табл. 6.2).
Таблица 6.2 - Расчет затрат и потерь
Перенесем полученные данные в платежную матрицу затрат (см. табл. 6.3.) и воспользуемся формулой для расчета bi. Таблица 6.3 - Матрица затрат
Поскольку в данной задаче эффективное решение выбирается по минимуму затрат, а не по максимуму прибыли, то Y* Ü min bi, следовательно Y* = Y2 (следует послать на завод ЖБИ свой транспорт и не предпринимать иных действий). ЗАДАЧА 7 «Построение дерева решений при определении продуктовой стратегии фирмы и стратегии развития ее производственных мощностей» Условие. Начальник ДСКа, в настоящее время выпускающего некоторую продукцию X1 в текущем объеме V1тек, считает, что расширяется рынок продукции Х2. Были проведены маркетинговые исследования, определившие уровни спроса на продукцию X1 и Х2 (V1max, V1min; V2max, V2min, соответственно) и вероятности высокого и низкого спроса (P1max, P1min = 1 – P1max; P2max, P2min = 1 – P2max). Установлено, что действующие мощности ДСКа могут быть использованы для производства продукции обоих видов. Известна прибыль на единицу продукции каждого вида (П1 и П2). Рассчитаны затраты (К) на удвоение мощности ДСКа (для параллельного производства продукции X1 в текущем объеме и продукции Х2 в эквивалентном количестве), на увеличение мощности комбината под максимальный спрос на текущую продукцию Х1 (K1) и под максимальный спрос на продукцию Х2 (соответственно К2). Цифровые данные следующие: V1тек = 1000 единиц; П1 = 0,001 ден.ед; V1max = 10000 единиц; K1 = 2 ден. ед.; V1min = 5000 единиц; V2экв = 900 единиц; П2 = 0,0009 ден. ед.; V2max = 8000 единиц; К2 = 1,2 ден. ед.; V2min = 4000 единиц; К = 0,4 ден. ед.; P1max = 0,7; P1min =1 – 0,7 = 0,3; P2max = 0,6; Р2min = 1 – 0,6 = 0,4. Требуется определить целесообразность замены продукции и развития мощностей, в том числе под одновременный выпуск продукции. Методические рекомендации по решению. Представим ход решения в виде дерева, наложенного на таблицу, и рассчитаем последствия решений (см. рис. 7.1). Установив последствия решений при выпуске продукции одного вида (Х1 и Х2), определим рациональные действия во 2-й точке принятия решений. Для этого вычеркнем нерациональные действия (точнее, бездействие по поводу развития мощностей) и перенесем данные об ожидаемом выигрыше в 4-ю графу. Далее с учетом вероятности спроса на продукцию рассчитываем среднюю эффективность действий в точках разветвления событий (3-я графа). Оказывается, что продолжить выпуск продукции X1 при одновременном развитии мощностей выгоднее, чем перейти на выпуск продукции Х2 вместо X1. Однако мы не учли возможность одновременною выпуска продукции Х1 и Х2 при развитии мощностей ДСКа под максимальный спрос. Поэтому из первой точки принятия решения проведем еще одну ветвь, соответствующую данному варианту решения. Его эффективность, складывается из эффективности первого и второго вариантов за вычетом затрат на первоначальное удвоение мощностей. Эффективность данного варианта является наиболее высокой, поэтому первые два варианта следует вычеркнуть. Общий вывод: требуется существенное развитие мощностей и одновременный выпуск двух видов продукции. Данная схема решения несколько упрощена, поскольку нами не рассматривались варианты меньшего развития мощностей, использования резервов по выпуску продукции одного вида при низком уровне спроса для выпуска другой продукции, ограничения по капиталовложениям (для этого в условиях задачи недостает данных).
ЗАДАЧА 8 «Выбор решения в условиях неопределенности и количественной шкалы оценок» Условие. Исходные данные аналогичны задаче 3, но без известной вероятности событий (см. табл. 8.1). Таблица 8.1 - Платежная матрица (количественная шкала – прибыли)
Требуется выбрать наилучшие решения по известным критериям оценки для разных стратегий ЛПР. При расчете по критерию Гурвица принять долю пессимизма h. Методические рекомендации по решению. Решение по критерию Вальда (максимину) представлено в табл. 8.2а. Таблица 8.2а
Таблица 8.2б
Для решения по критерию Сэвиджа (минимаксу), сформируем матрицу потерь (см. табл. 8.2б). Решение по критерию оптимизма (максимакса) дано в табл. 8.2в. Таблица 8.2в
Решение по критерию Гурвица представлено в табл. 8.3 (в нем использованы значения Таблица 8.3 - Выбор решения по критерию Гурвица при h = 0,4
Итоговые данные по вариантам решения задач для разных стратегий и критериев приведены в табл. 8.4. Таблица 8.4 - Итоги решения задач
Анализ итогов показывает, что результаты выбора зависят не только от полноты данных и избранной стратегии ЛПР, но и от непосредственного выбора критерия оценки и доли пессимизма в критерии Гурвица. ЗАДАЧА 9 «Определение эффективных решений» Условие. Пусть имеются четыре допустимые решения, и групповое ЛПР состоит из двух членов с функциями предпочтения Ф1 и Ф2, соответственно. Оба ЛПР провели упорядочение решений следующим образом: Ф1 : Ф2: В соответствии с этим упорядочением значения функций предпочтения, измененные в рангах, представлены в табл. 9.1 Таблица 9.1 - Предпочтения членов группы
Требуется определить эффективные решения, используя принцип Парето. Методические рекомендации по решению. Задача иллюстрирует, как из множества допустимых (приемлемых, удовлетворяющих ограничениям) решений методом логического анализа осуществляется отбор эффективных недоминирующих решений. Эффективные решения между собой несравнимы, так как нельзя сказать, какое из них предпочтительнее. Эффективные решения составляют «множество Парето», из которого уже иным способом выбирается оптимальное (единственное, наилучшее) с привлечением дополнительной информации (вероятности событий, значимости целей, веса членов группового ЛПР. Общая формула отбора: Y Ê Yд Ê Yэ Ê Y*, где Y – множество альтернативных решений. Yд – множество допустимых решений. Yэ – множество эффективных решений, Y* - оптимальное решение. Осуществляя выделенный этап отбора решений, будем сравнивать последовательно пары решений по предпочтительности. Решения Y1 и Y2, как это следует из таблицы ранжировок, между собой несравнимы, так как мнения группы по их приоритету разделились. В то же время оба члена группы считают, что решения Y1 и Y3 находятся в отношении Для наглядности процедуры определения эффективных решений представим все решения как точки на плоскости в системе координат Ф1 и Ф2. На рис. 9.1 по оси Ф1 отложены предпочтения первого члена группы, а по оси Ф2 – предпочтения второго члена группы. Измерения предпочтений проведены в порядковой шкале, в которой нет понятий масштаба и начала отсчета, поэтому точки на осях координат, характеризующие ранги, могут быть расположены неравномерно при соблюдении единственного условия
Рисунок 9.1 – Графическая оценка предпочтений решений ЗАДАЧА 10 «Оценка согласованности мнений экспертов» Условие. Результаты ранжирования шести управленческих решений (объектов оценки) пятью экспертами представлены в табл. 10.1. Таблица 10.1 - Результаты ранжирования m = 6 объектов d = 5 экспертами (rij - ранг i-го объекта / решения, присвоенный j-м экспертом)
Требуется оценить согласованность мнений экспертов. Методические рекомендации по решению. Согласованность оценок экспертов характеризуется двумя показателями: величиной коэффициента конкордации W и наблюдаемым распределением частот (расчетной вероятностью) f2. Дисперсный коэффициент конкордации W характеризует достоверность итоговой оценки (согласованность мнений экспертов и сходимость результатов); он рассчитывается по формуле:
S – сумма квадратов отклонений оценок от математического ожидания (среднего значения) суммарного ранга одного объекта:
m - число объектов ранжирования (m = 6); d - число экспертов (d = 5); i - индекс объекта; j - индекс эксперта; ri,j - ранг, присвоенный i-му объекту j-м экспертом (см. табл. 4.18); Tj - показатель связанных рангов в ранжировке j-ro эксперта:
k - номер группы связанных (равных) рангов; Hj - число групп связанных рангов в ранжировке j-ro эксперта; hk - число равных рангов в k-й группе связанных рангов Если в ранжировках совпадающих рангов нет, то все Hj = 0; hk = 0 и, следовательно, Tj = 0; в этом случае формула 10.1 принимает вид:
Величина W = 1 характеризует полное совпадение мнений; W = 0 - свидетельствует, что все ранжировки разные. Показатель наблюдаемого распределения частот f2 применяется для с
|

 (4.1)
(4.1) 1 при fi,j £ fk,j
1 при fi,j £ fk,j
 (5.1)
(5.1) . Если элемент сравнивается сам с собой (k = i), т.е. он не хуже себя, то проставляется единица; если он выше по рангу (меньше по величине), чем i-й элемент, то проставляется ноль; если он равен или ниже по рангу, то Хji,k равен единице. Таким образом, X11,1 = 1(1 = 1); X12,1 = 0 (2 > 1); X13,1 = 0 (3 > 1). Аналогично оцениваются значения X1i,k для k = 2 и 3. Матрица
. Если элемент сравнивается сам с собой (k = i), т.е. он не хуже себя, то проставляется единица; если он выше по рангу (меньше по величине), чем i-й элемент, то проставляется ноль; если он равен или ниже по рангу, то Хji,k равен единице. Таким образом, X11,1 = 1(1 = 1); X12,1 = 0 (2 > 1); X13,1 = 0 (3 > 1). Аналогично оцениваются значения X1i,k для k = 2 и 3. Матрица 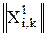 приведена в табл. 5.2,а. Так же рассчитываем значения элементов X2i,k и X3i,k – см. табл 5.2,б и 5.2, в.
приведена в табл. 5.2,а. Так же рассчитываем значения элементов X2i,k и X3i,k – см. табл 5.2,б и 5.2, в. 1 при
1 при  ;
; = (5.2)
= (5.2) ;
; (5.3)
(5.3) , а затем оценка элементов Yi,k – см. табл. 5.3.
, а затем оценка элементов Yi,k – см. табл. 5.3. (j = 1) (j = 2) (j = 3) (S)
(j = 1) (j = 2) (j = 3) (S)

 :
:




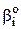 из табл. 8.2а и 8.2в).
из табл. 8.2а и 8.2в).



 ; (9.1)
; (9.1) Y4
Y4 , поэтому решение Y1 не может быть эффективным, поскольку есть доминирующее лучшее решение Y3. Следовательно, решение Y1 исключается из дальнейшего рассмотрения. Оба члена группы считают, что
, поэтому решение Y1 не может быть эффективным, поскольку есть доминирующее лучшее решение Y3. Следовательно, решение Y1 исключается из дальнейшего рассмотрения. Оба члена группы считают, что  , поэтому решение Y4 также является неэффективным. Таким образом, из исходного множества четырех решений остались всего два решения Y2 и Y3, которые и будем считать эффективными, не отдавая предпочтения ни одному из членов группы.
, поэтому решение Y4 также является неэффективным. Таким образом, из исходного множества четырех решений остались всего два решения Y2 и Y3, которые и будем считать эффективными, не отдавая предпочтения ни одному из членов группы. . Эффективные решения Y2 и Y3 обведены на рисунке контуром.
. Эффективные решения Y2 и Y3 обведены на рисунке контуром.
 , где (10.1)
, где (10.1) ; (10.2)
; (10.2) - математическое ожидание суммарного ранга одного объекта:
- математическое ожидание суммарного ранга одного объекта: (10.3)
(10.3) ; (10.4)
; (10.4) .
.


