ЗАДАЧА 15
У банка имеются два должника, значения КТЛ у которых за три прошедших месяца составили: у первого – К11 = 1.5, К12 = 1.3, К13 = 1.7 и у второго – К21 = 1.6, К22 = 1.4 и К23 = 1.5. Используя Лемму Маркова и неравенство Чебышева необходимо определить, какова вероятность (Р) того, что они в течение ближайшего месяца погасят свои долги перед банком? Рекомендации по решению Среднее значение КТЛ у обоих должников равно одной и той же величине: 1,5. В силу этого лемма Маркова здесь показала бы совершенно одинаковую вероятность погашения долга у двух должников: Р(Х ³ 2) < Вероятность же невозврата долга у обоих по лемме Маркова здесь составила бы как минимум 25%. Неравенство Чебышева даст разные значения этих вероятностей для упомянутых должников, ибо оно кроме среднего уровня КТЛ учитывает еще и его колеблемость, которая у первого больше, чем у второго, что видно по величине дисперсий:
Упомянутые должники погасят свой долг перед банком, если восстановят свою платежеспособность, т.е. повысят свой КТЛ до уровня 2. Для этого он у них должен будет отклониться в большую сторону от нынешнего своего значения как минимум на 0.5. Вероятность такого отклонения в обе стороны по неравенству Чебышева равна: для первого должника - Р(|х -1.5| > 0.5) < для второго - Р(|х -1.5| ³ 0.5) < Как, как уже отмечалось, нужна вероятность отклонения только в одну – большую сторону. Она составит для первого должника меньше 10.68%: 2 = 5.34%; для второго должника меньше 2.68%: 2 = 1.34%. Таким образом, вероятность невозврата долга первым должником будет как минимум 100 – 5.34 = 94.66%, а вторым – как минимум 100 – 1.34 = 98.66%. Почему должник с меньшей колеблемостью вернет ссуду с меньшей вероятностью? Ведь чем ниже колеблемость, тем выше, казалось бы, должна быть его надежность! Объясняется все это очень просто. В данном примере меньшая колеблемость КТЛ у второго должника говорит о его большей устойчивости в состоянии неплатежеспособности. Быть устойчивым неплательщиком – отнюдь не положительное качество. Поэтому и вероятность невозврата им долга оказалась выше. Если бы у него была меньшая колеблемость вблизи значения КТЛ, равного, например, 2.5, тогда все обстояло бы у него по-другому. Но он «застрял» на КТЛ куда меньше 2. Большим достоинством леммы Маркова и неравенства Чебышева остается то, что они пригодны для употребления при любом количестве наблюдений и любом законе распределения вероятностей. Платой за отсутствие жестких ограничений является некоторая неопределенность оценок уровня вероятности, причем при использовании леммы Маркова она значительно больше, чем при применении неравенства Чебышева.
|

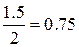 , т.е. менее 75%
, т.е. менее 75%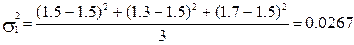
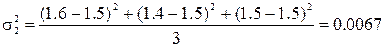

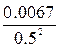 = 0.0268.
= 0.0268.


