ЗАДАЧА 17
Эксперты определили надежность банка А на уровне Р(А) = 90%, а банка В – на уровне Р(В) = 80%. Следовательно они считают, что банк А может оказаться банкротом с вероятностью в того, что оба банка не станут банкротами – Р(АиВ); 2) банкротства двух банков – 3) банкротства только банка А – 4) банкротства только банка В – 5) банкротства только одного какого-нибудь банка (или банка А, или банка В) – 6) наступления хотя бы одного банкротства – 7) Проверить, что полная группа событий (полное отсутствие банкротств, банкротство только для одного банка, банкротство сразу двух банков) равно 1,0. Рекомендации по решению Согласно теореме умножения, вероятность того, что оба банка не станут банкротами, здесь будет равна Р(А и В) = Р(А) × Р(В) = 0.9 × 0.8 = 0.72. Вероятность же того, что оба банка станут банкротами составит Р( Здесь Вероятность того, что банкротом станет только банк А, а банк В продолжит свою деятельность, будет равна
Вероятность банкротства только банка В составит
Заметим, что вероятность одновременного банкротства сразу двух банков многократно меньше вероятности банкротства каждого из них в отдельности (0.02 против 0.10 или 0.20). Значит, если надо во что бы то ни стало избежать потери всех средств, следует помещать их не в один, пусть самый надежный банк, а в несколько банков. Это называется диверсификацией. Иной раз она может несколько снизить доход, зато повышает гарантию сохранности хотя бы части средств, т.е. помогает инвесторам избежать при рискованных инвестициях полного финансового краха. Как уже отмечалось, теорема сложения вероятностей позволяет определять вероятность наступления или события А, или события В. Согласно ей, вероятность банкротства только одного какого-нибудь банка (или банка А, или банка В) равна
От понятия наступление только одного банкротства надо отличать понятие наступление хотя бы одного банкротства. Вероятность последнего (или банка А, или банка В, или сразу двух) составит по формуле суммы вероятностей для совместных событий
Этот же результат можно также получить, суммируя ранее найденные вероятности банкротства только одного какого-нибудь банка и банкротства сразу двух банков: 0.26 + 0.02 = 0.28. Наконец, ту же самую цифру можно получить как вероятность события, противоположного отсутствию всяких банкротств: 1 – 0.72 = 0.28. Полную группу событий в данном примере составляет следующий перечень событий: полное отсутствие банкротств, банкротство только для одного банка, банкротство сразу двух банков. Сумма их вероятностей равна единице: 0.72 + 0.26 + 0.02 = 1.
|

 = 10%, а банк В с вероятностью
= 10%, а банк В с вероятностью  = 20%. Определить вероятность:
= 20%. Определить вероятность: ;
; ;
; ;
; ;
;
 и
и  ) = 0.1 × 0.2 = 0.02.
) = 0.1 × 0.2 = 0.02. = 0.1 × 0.8 = 0.08.
= 0.1 × 0.8 = 0.08. = 0.9 × 0.2 = 0.18.
= 0.9 × 0.2 = 0.18.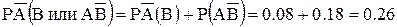 .
. .
.


