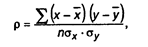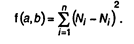Корреляционно-регрессионный анализ. Корреляционно-регрессионный анализ — классический метод стохастического моделирования хозяйственной деятельности
Корреляционно-регрессионный анализ — классический метод стохастического моделирования хозяйственной деятельности. Он изучает взаимосвязи показателей хозяйственной деятельности, когда зависимость между ними не является строго функциональной и искажена влиянием посторонних, случайных факторов. При проведении корреляционно-регрессионного анализа строят различные корреляционные и регрессионные модели хозяйственной деятельности. В этих моделях выделяют факторные и результативные показатели (признаки). В зависимости от количества исследуемых показателей различают парные и многофакторные модели корреляционно-регрессионного анализа. Основной задачей корреляционно-регрессионного анализа является выяснение формы и тесноты связи между результативным и факторным показателями. Под формой связи понимают тип аналитической формулы, выражающей зависимость результативного показателя от изменений факторного. Различают связь прямую, когда с ростом (снижением) значений факторного показателя наблюдается тенденция к росту (снижению) значений результативного показателя. В противном случав между показателями существует обратная связь. Форма связи может быть прямолинейной (ей соответствует уравнение прямой линии), когда наблюдается тенденция равномерного возрастания или убывания результативного показателя, в противном случае форма связи называется криволинейной (ей соответствует уравнение параболы, гиперболы и др.). ОСНОВНЫЕ МОДЕЛИ КОРРЕЛЯЦИОННОГО АНАЛИЗА. Такими моделями являются: коэффициент парной корреляции, коэффициент частной корреляции, коэффициент множественной корреляции, коэффициент детерминации. Линейный коэффициент парной корреляции (р) определяется по формуле:
где х, у — значения факторного и результативного показателей соответственно; х, у — средние значения соответствующих показателей; σ X, σ Y - средние квадратические отклонения (стандартные отклонения показателей х и у);
n — количество наблюдений в совокупности. Значение коэффициента парной корреляции изменяется в пределах от -1 до +1. Знак «+» означает наличие прямой связи между показателями. Знак «-» — наличие обратной связи. Значение коэффициента от 0 до 1 характеризует степень приближения корреляционной зависимости между показателями и к функциональной. При р = 1 между показателями существует функциональная связь. При р = 0 линейная связь отсутствует. В целях упрощения расчетов на практике применяются и другие формулы коэффициента парной корреляции, представляющие собой некоторые преобразования исходной формулы. Часто в анализе хозяйственной деятельности при изучении связи между показателями х и у требуется исключить воздействие третьего показателя z, выступающего как общий фактор изменения анализируемых показателей. Для этого используется коэффициент частной корреляции (rx,y,z), свойства которого совпадают со свойствами коэффициента парной корреляции:
где rxy, rxz, ryz — коэффициенты парной корреляции между соответствующими показателями. Коэффициент множественной корреляции (R) характеризует тесноту связи между результативным показателем и набором факторных показателей:
где σ2 — общая дисперсия эмпирического ряда, характеризующая общую вариацию результативного показателя (у) за счет факторов; σ ост 2— остаточная дисперсия в ряду у, отражающая влияния всех факторов, кроме х; у — среднее значение результативного показателя, вычисленное по исходным наблюдениям; s — среднее значение результативного показателя, вычисленное по уравнению регрессии. Коэффициент множественной корреляции принимает только положительные значения в пределах от 0 до 1. Чем ближе значение коэффициента к 1, тем больше теснота связи. И, наоборот, чем ближе к 0, тем зависимость меньше. При значении R < 0,3 говорят о малой зависимости между величинами. При значении 0,3 < R <; 0,6 говорят о средней тесноте связи. При R > 0,6 говорят о наличии существенной связи. Квадрат коэффициента множественной корреляции называется коэффициентом детерминации (D): D = R2. Коэффициент детерминации показывает, какая доля вариации результативного показателя связана с вариацией факторных показателей. В основе расчета коэффициента детерминации и коэффициента множественной корреляции лежит правило сложения дисперсий, согласно которому общая дисперсия (σ2) равна сумме межгрупповой дисперсии (δ2) и средней из групповых дисперсий σi2): σ2 = δ2 + σi2. Межгрупповая дисперсия характеризует колеблемость результативного показателя за счет изучаемого фактора, а средняя из групповых дисперсий отражает колеблемость результативного показателя за счет всех прочих факторов, кроме изучаемого. Математические модели корреляционного анализа в форме коэффициентов имеют ограниченные аналитические возможности. Зная лишь направление ковариации показателей и тесноту связи, невозможно определить закономерности формирования уровня результативного показателя под влиянием исследуемых факторов, оценить интенсивность их влияния, классифицировать факторы на основные и второстепенные. Для этих целей используются модели регрессионного анализа. Линейная модель (уравнение) регрессионного анализа может быть представлена в виде у = bo + b 1 x 1+ b 2 x 2 +... + bnxn, где у — результативный показатель; x 1, x 2,..., xn — факторные модели; b 0, b 1, b 2, ..., bn — коэффициенты регрессии. Коэффициенты регрессии показывают интенсивность влияния факторов на результативный показатель. Если проведена предварительная стандартизация факторных показателей, то b 0 равняется среднему значению результативного показателя в совокупности. Коэффициенты b 1, b 2, ..., bn показывают, на сколько единиц уровень результативного показателя отклоняется от своего среднего значения, если значения факторного показателя отклоняются от среднего, равного нулю, на одно стандартное отклонение. Таким образом, коэффициенты регрессии характеризуют степень значимости отдельных факторов для повышения уровня результативного показателя. Конкретные значения коэффициентов регрессии определяют по эмпирическим данным согласно методу наименьших квадратов (в результате решения систем нормальных уравнений). Аналитические достоинства регрессионных моделей заключаются в том, что, во-первых, точно определяется фактор, по которому выявляются резервы повышения результативности хозяйственной деятельности; во-вторых, выявляются объекты с более высоким уровнем эффективности; в-третьих, возникает возможность количественно измерить экономический эффект от внедрения передового опыта, проведения организационно-технических мероприятий. Рассмотрим теперь задачу 1 из заданий по анализу регрессии, приведенную на с. 300—301. Построим линейную регрессионную модель по методу наименьших квадратов. Обозначим через t i, год выпуска автомобилей, а через N i — объем выпуска в этом году. Данные, представленные в таблице, изобразим на графике, представленном ниже. В качестве функции линейной регрессии возьмем N i = а + bt i, i = 1,2,...,32. Критерий метода наименьших квадратов в этом случае имеет вид
Выпуск автомобилей по годам (N — тыс. шт.)
Один из математических результатов теории линейной регрессии говорит, что оценка N, является несмещенной оценкой с минимальной дисперсией в классе всех линейных несмещенных оценок.
Остаточная дисперсия вычисляется по формуле
Современный факторный анализ — направление многомерного статистического анализа, которое позволяет выявить внутренние, непосредственно неизмеримые переменные (факторы) между коррелирующими показателями хозяйственной деятельности. Различают два основных метода современного факторного анализа: метод главных компонент и классический факторный анализ. Модель метода главных компонент выглядит так: zj = aj 1 F 1 + aj 2 F 2 +...+ ajnFn, где zj — исходные показатели; F 1, F 2, ..., Fn — компоненты (факторы); ajn — факторные нагрузки на j -ю переменную. Модель классического факторного анализа выглядит несколько иначе: zj = aj 1 F 1 + aj 2 F 2 +...+ ajmFm + ajFj + uj, где исходная переменная zj линейно зависит от m общих факторов F 1, F 2, ..., Fm (обычно m намного меньше n) и характерного фактора иj. Общие факторы описывают корреляции между параметрами, характерный фактор учитывает оставшуюся дисперсию исходных показателей. Основные этапы современного факторного анализа: • качественный предварительный анализ экономических явлений и постановка задачи факторного анализа; • составление массивов исходной информации; • вычисление и анализ начальной корреляционной матрицы; • нахождение прямого факторного решения; • нахождение интерпретируемого факторного решения: • вычисление факторных коэффициентов; • содержательная интерпретация факторов; • анализ и использование полученных результатов. (При помощи такого анализа выявляют и измеряют независимые скрытые факторы для построения аналитической модели.); • выявление наиболее информативных показателей деятельности; • соединение информации о независимых аспектах явления в один обобщающий показатель; • классификация и ранжирование объектов по обобщающим факторам; • комплексная оценка хозяйственной деятельности.
|