Вопрос 25 Потенциал
Работа консервативны сил совершается за счет убыли потенциальной энергии. Работу сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд Q в начальной и конечной точках поля заряда Q:
Отношение U/Q Потенциал Потенциал поля, создаваемого точечным зарядом Q, равен Работа, совершаемая силами электростатического поля при перемещении заряда Q
т. е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках. Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами поля при перемещении положительного единичного заряда из точки 1 в точку 2.
где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения. Если перемещать заряд Q A откуда
Таким образом, потенциал — физическая величина, определяемая работой по перемещению положительного единичного заряда при удалении его из данной точки поля в бесконечность. Единица потенциала — вольт (В): 1 В есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В= 1 Дж/Кл). Если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов. Элементарная работа сил электростатического поля переноса положительного единичного точечного заряда на пути dl равна E d l = E Интеграл Формула справедлива только для электростатического поля.
|

 =
= 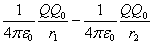 = U
= U 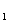 -U
-U 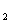
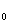 не зависит от Q
не зависит от Q 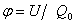
 в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией положительного единичного заряда, помещенного в эту точку.
в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией положительного единичного заряда, помещенного в эту точку.
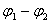 ), не зависит от траектории перемещения
), не зависит от траектории перемещения
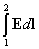 =
= 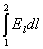
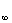 = Q
= Q  dl, где E
dl, где E 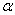 — проекция вектора Е на направление элементарного перемещения.
— проекция вектора Е на направление элементарного перемещения. называется циркуляцией вектора напряженности. Циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю, следовательно, линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и заканчиваются на зарядах или же уходят в бесконечность.
называется циркуляцией вектора напряженности. Циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю, следовательно, линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и заканчиваются на зарядах или же уходят в бесконечность.


