Уравнение неразрывности. Рассмотрим установившееся течение
u1dS1 = u2dS2. (1) Для других сечений струйки можно получить такие же соотношения: u1dS1 = u2dS2 = u3dS3 = … = undSn = const = dQ. Данное уравнение выражает условие неразрывности для элементарной струйки, из которого видно, что через все ее сечения в единицу времени протекает один и тот же объем жидкости. Имеет место:
Таким образом, скорости течения в двух сечениях элементарной струйки обратно пропорциональны площадям этих сечений. Проинтегрируем уравнение (1) по соответствующим сечениям:
По определению средней скорости: v1S1 = v2S2, а для любых сечений: v1S1 = v2S2 = v3S3 = … = vnSn = const =Q. (2) Это уравнение неразрывности потока, которое показывает, что объемный расход несжимаемой жидкости при установившемся движении сохраняется постоянным вдоль всего потока и равен произведению площади живого сечения потока на среднюю скорость. Из уравнения (2) следует:
т.е. средние скорости потока обратно пропорциональны площадям соответствующих сечений.
|
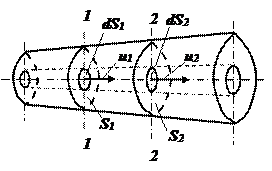Рассмотрим установившееся течение. Выделим в потоке элементарную струйку и рассмотрим участок между сечениями 1-1 и 2-2. За время dt в выделенный участок войдет количество жидкости, равное объему цилиндра высотой u1dt и площадью основания dS1, т.е. dV1=u1dtdS1. Аналогично, через сечение 2-2 вытекает объем жидкости dV2=u2dtdS2. в силу несжимаемости и сплошности жидкости dV1= dV2, т.е.:
.
.
,
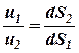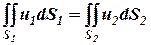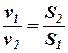