Модель авторегрессии и скользящего среднего ARMA(p,q).

Оценивание параметров данной модели базируется на статистическом оценивании параметров модели с помощью методов моментов.

Рассмотрим один из алгоритмов оценки параметров:

1 этап:

Перепишем модель в виде:

Х_t- [f₀]-f₁∙Х_t-1- f₂∙Х_t-2- …-f_р∙Х_t-р = e_t - w₁∙e_t-1- w₂∙e_t-2- …-w_q∙e_t-q.

Домножим правую и левую части на X_t-q-1, X_t-q-2,…, X_t-q-p и перейдем к мат.ожиданиям в каждом из р полученных таким образом соотношений. После деления каждого соотношения на s²_х получим следующую систему линейных уравнений относительно f₁ ,..., f_р:

2 этап:

Подставим найденные оценки в исходное уравнение и «протиражируем» получившееся соотношение для моментов времени t, t+1, t+2, …, t+q. В результате получим следующий набор из (q+1) соотношений:

Затем обе части 1-ого уравнении поочередно домножим на самих себя, на 2-ое, 3-е уравнение и т.д. После перехода к мат.ожиданиям в левой части каждого из (q+1) уравнения, будут находиться различные комбинации автоковариаций и оценок , а правые части будут представлять собой некоторые нелинейные комбинации от неизвестных параметров: s²_х, w₁, w₂,..., w_q. Решив эту систему найдем оценки параметров: s²_х, w₁, w₂,..., w_q.

Оценим параметры модели ARMA(1,1): Х_t= f₁∙Х_t-1+ e_t - w₁∙e_t-1

1-ый этап: .

2-ой этап:

 

Решив данное уравнение относительно , выбираем корень, который удовлетворяет условию: 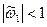. Затем определяем s²_e.