Выявление нестационарности ряда (тесты на идентификацию).

В основу одного из подходов положена проверка условия равенства или неравенства параметра a₁ (из уравнения: Х_t=a₀ +a₁∙X_t-1 +e_t) единице. То есть проверяется гипотеза Н0: a₁=1 (ряд нестационарный) при альтернативной гипотезе Н1: a₁<1 (ряд стационарный). Это так называемые тесты на единичный корень. Проверка осуществляется с помощью t-статистики Стьюдента.

Другие гипотезы формулируются о стационарности временного ряда и их большинство, несмотря на то, что большинство реальных временных рядов нестационарные. Однако путем взятия конечных разностей нестационарные временные ряды можно преобразовать в стационарные.

Метод разностей и интегрируемость.

Первые разности: ∆Х_t =X_t – X_t-1. Если окажется, что ряд ∆Х_t стационарен, то ряд Х_t называют интегрируемым 1-ого порядка.

Если же ряд ∆Х_t нестационарен, то берут вторые разности: ∆²Х_t =∆X_t – ∆X_t-1. Если окажется, что ряд ∆²Х_t стационарен, то ряд Х_t называют интегрируемым 2-ого порядка.

Если же и ряд ∆²Х_t нестационарен, то берут третьи разности: ∆³Х_t =∆²X_t – ∆²X_t-1и т.д. пока не получат стационарный ряд из конечных разностей.

Если мы получаем первый стационарный ряд после взятия k-кратного взятия разностей, процесс называется интегрируемым k-ого порядка.

Оценка порядка интегрируемости.

1. С помощью интегрируемой статистики IDW (Дарбина-Уотсона):

Н0: ряд нестационарен

Н1: ряд стационарен

Для проверки используют интегрируемую статистику IDW:

.

Если окажется, что IDWÎ[0; IDW_L], то гипотезу Н0 не отвергаем.

Если окажется, что IDWÎ[IDW_U;2], то гипотезу Н1 не отвергаем.

Если окажется, что IDWÎ[IDW_L;IDW_U], то определенного вывода сделать не представляется возможным.

3. Тесты Дики-Фуллера - DF или тесты на единичный корень (базовый метод для определения интегрируемости).

Пусть d=f₁-1. Тогда: Х_t-Х_t-1 = ∆Х_t = d∙Х_t-1 + e_t.

Это эквивалентно: Х_t =(1+d)∙Х_t-1 + e_t.

Н0: ряд нестационарный d³0 (f₁=1)

Н1: ряд стационарный 0-ого порядка d<0 (f₁<1) (т.е. левосторонняя критическая область).

Параметр d из уравнения: ∆Х_t = d∙Х_t-1 + e_t оценивается с помощью обычного МНК. Для оценки значимости параметра рассчитывается наблюдаемое значение статистика критерия по формуле t-статистики Стьюдента. Критическое значение находят с помощью статистических таблиц, содержащих пороговые значения DF-статистики. Если t наблюдаемое меньше t табличного, то гипотезу Н0 следует отвергнуть и принять гипотезу Н1.

В случае, если t наблюдаемое больше t табличного, то гипотезу Н0 не отвергают, следовательно можно утверждать, что процесс Х_t нестационарен. Из этого следует дополнительный вывод: либо процесс Х_t интегрируем более высокого порядка, чем нулевой, либо неинтегрируем вообще.

Следующий этап в оценке порядка интегрируемости временного ряда – проверка гипотезы о том, что Х_t интегрируемый процесс 1-ого порядка. Если Н0 не может быть отклонена, то следует проверить Х_t на интегрируемость 2-ого порядка.

На практике редко встречаются процессы интегрируемые выше 2-ого порядка.

Модификация теста Дики-Фуллера для случая автокорреляции в остатках – ADF(k).

∆Х_t = d∙Х_t-1 + Sa_i∙Х_t-i +e_t.

С помощью t-критерия Стьюдента оценивается значимость a_i. Слагаемые с незначимыми параметрами отбрасываются.

Критерий выбора оптимальной длины лага – информационные критерии Акаике и Шварца:

AIC= .

SC= .

Лучше та модель, для которой критерии Акаике и Шварца меньше.
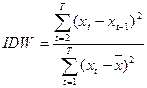