Оценивание параметров моделей ARMA.1. Модель авторегрессии. В случае АR(1): Хt= [f0]+f1∙Хt-1+ et, где et – «белый шум» с μe=0. Если имеется константа f0, то мат.ожидание процесса будет равно f0. Следовательно, оценка данного параметра будет равна среднему арифметическому:
Оценкой параметра f1 будет выборочный коэффициент автокорреляции 1-ого порядка:
В случае АR(2): Хt= [f0]+f1∙Хt-1+f2∙Хt-2+et, где et – «белый шум» с μe=0. Оценками параметров f1 и f2 будут:
Где
Рассмотрим теперь общий случай авторегрессии: АR(p): Хt= [f0]+f1∙Хt-1+ f2∙Хt-2+ …+fр∙Хt-р+ et, где et – «белый шум» с μe=0. Для оценки параметров fj (j =1;p) нужно решить систему уравнений:
2. Модель скользящего среднего: В случае МА(1): Хt=et - w1∙et-1, где et – «белый шум» с μe=0 требуется оценить один параметр w1. Для его оценки воспользуемся формулой коэффициента автокорреляции 1-ого порядка: Если оценить r1 как выборочный коэффициент автокорреляции:
то оценки параметра можно найти из соотношения (*):
Т.е. нужно найти корни квадратичного уравнения. Их всего будет два. Выбирают тот корень, который удовлетворяет неравенству: │w1│<1 (условие обратимости для МА(1)). В случае МА(2): Хt=et - w1∙et-1- w2∙et-2, где et – «белый шум» с μe=0 требуется оценить два параметра: w1, w2. Для оценки параметров воспользуемся формулами расчета коэффициентов автокорреляции 1-ого и 2-ого порядков:
Подставляя вместо коэффициентов автокорреляции их выборочные оценки и решив систему нелинейных уравнений (**) получим искомые оценки w1, w2. В случае МА(3): Хt=et - w1∙et-1- w2∙et-2-w3∙et-3, где et – «белый шум» с μe=0 требуется оценить два параметра: w1, w2, w2. Для оценки параметров воспользуемся формулами расчета коэффициентов автокорреляции 1-ого, 2-ого и 3-его порядков:
Подставляя вместо коэффициентов автокорреляции их выборочные оценки и решив систему нелинейных уравнений (***) получим искомые оценки w1, w2, w2.
|
;
; 
.
- выборочный коэффициент автокорреляции порядка t: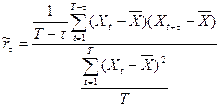
.
(*).
,
.
(**).
(***).
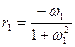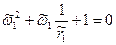