Круглый волновод
В круглом волноводе электромагнитное поле представляется в виде совокупности поперечно – электрических (Н – волны) и поперечно – магнитных (Е - волны) различных типов. Так же и в теории прямоугольных волноводов, из уравнений Максвелла можно получить волновое уравнение для
где
Как и в предыдущем анализе рассматриваем гармонические колебания, волна распространяется вдоль оси Z, т. е. Решение волнового уравнения в цилиндрической системе координат представляется совокупностью функций Бесселя и гармонических функций.
Функции Бесселя второго рода
Так как функция
Таким образом, делаем вывод, что граничное условие выполнимо при обращении производных соответствующих производных функций Бесселя в нуль, т. е. аргумент функции
Индекс m определяет порядок функции Бесселя, а n – номер её корня. В структуре поля m определяет число полуволн вдоль диаметра волновода, а n – вдоль его окружности, т. е. число вариаций по диаметру и по азимуту. Аналогичный анализ можно провести и для Е – волн, в этом случае условие распространения поля определяется
где В круглом волноводе основной является волна
Таблица В1
Особый интерес представляет в круглом волноводе волна
РИСУНОК Гольдштейн, Зернов стр. 446
Рис. 6.5 – Зависимость затухания волн от частоты в круглом волноводе. Это объясняется следующим образом. Все типы волн, кроме Однако волна Для повышения устойчивости этой волны используются не сплошные волноводы, а спиральные, тогда кольцевые токи смещения поддерживаются спиральными токами в стенках волновода. Спиральные волноводы имеют большее затухание, чем сплошные, поэтому на практике в круглых волноводах используются вставки из спиральных волноводов. Волноводы непосредственно для организаций линий связи не применяются, т. к. они имеют ряд недостатков. Они применяются в антенно – фидерных трактах в радиорелейной связи, в наземных станциях спутниковых систем связи.
Вопросы для самоконтроля 1. Какие классы и типы волн (моды) распространяются между двумя проводящими плоскостями? 2. Объясните смысл уравнения 6.4. 3. Объясните смысл граничных условий для составляющих поля. 4. Что такое критическая частота (длина волны)? 5. Чем определяется 6. Охарактеризуйте режим передачи в системе из плоско – параллельных плоскостей? 7. Объясните смысл уравнений 6.12. 8. Какие классы и типы волн распространяются в волноводах? 9. Чем определяется критическая частота (длина волны) в волноводе? 10. Объясните смысл индексов m и n. 11. Объясните смысл уравнения 6.20. 12. Каким условиям удовлетворяет распространение электрических и магнитных волн в круглом волноводе.? 13. Какой основной тип волны в круглом волноводе? 14. Объясните особенности волны 15. Объясните особенности спиральных волноводов.
|

 или
или  составляющих. Рассмотрим Н – волны, для которых волновое уравнение имеет вид
составляющих. Рассмотрим Н – волны, для которых волновое уравнение имеет вид , (6.18)
, (6.18) - поперечное волновое число,
- поперечное волновое число, 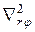 - оператор Лапласа в цилиндрической системе координат, тогда (6.18) запишется:
- оператор Лапласа в цилиндрической системе координат, тогда (6.18) запишется: (6.19)
(6.19) .
. (6.20)
(6.20) при
при  обращаются в бесконечность. Из физических условий ясно, что поле в центре волновода (
обращаются в бесконечность. Из физических условий ясно, что поле в центре волновода ( ) должно иметь конечное значение, т. е.
) должно иметь конечное значение, т. е.  . Тогда (В.20) будет иметь вид:
. Тогда (В.20) будет иметь вид: . (6.21)
. (6.21) не должна изменяться при замене
не должна изменяться при замене  на
на  , то
, то 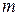 может быть лишь целым числом, т. е.
может быть лишь целым числом, т. е.  Для рассматриваемой системы должно выполняться граничное условие
Для рассматриваемой системы должно выполняться граничное условие  , при
, при 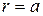 , это условие выполнимо при
, это условие выполнимо при при
при  ,
, 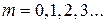
 является корнем производной функции Бесселя первого рода порядка
является корнем производной функции Бесселя первого рода порядка 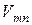 . Учитывая соотношение
. Учитывая соотношение 
 , определяем критическую частоту в круглом волноводе
, определяем критическую частоту в круглом волноводе . (6.22)
. (6.22) при
при  ,
, - n – ый корень функции Бесселя m – го порядка. Как видно из анализа, в круглом волноводе также распространяется бесчисленное множество (континуум) мод, условие распространения которых определяется обращением в нуль функций Бесселя (Е - волны) или их производных (Н - волны), а значения критических частот определяются значениями корней этих функций.
- n – ый корень функции Бесселя m – го порядка. Как видно из анализа, в круглом волноводе также распространяется бесчисленное множество (континуум) мод, условие распространения которых определяется обращением в нуль функций Бесселя (Е - волны) или их производных (Н - волны), а значения критических частот определяются значениями корней этих функций. , при радиусе волновода а она имеет наибольшую критическую длину волны
, при радиусе волновода а она имеет наибольшую критическую длину волны  . В этом смысле волна
. В этом смысле волна  является аналогом волны
является аналогом волны  в прямоугольном волноводе. В таблице 6.1 приведены структуры поля некоторых типов волн и их критические частоты.
в прямоугольном волноводе. В таблице 6.1 приведены структуры поля некоторых типов волн и их критические частоты.



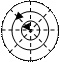
 ,
,  ,
,  ,
, 
 ,
, 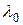






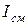 , в металлических стенках токи отсутствуют. С увеличением частоты силовые линии электрического поля концентрируются в центре волновода.
, в металлических стенках токи отсутствуют. С увеличением частоты силовые линии электрического поля концентрируются в центре волновода. в системе из проводящих бесконечных плоскостей?
в системе из проводящих бесконечных плоскостей?


