Поведение газа в центробежном поле сил
Рассмотрим поведение газа внутри вращающегося вокруг своей оси с постоянной угловой скоростью Ω цилиндра радиуса а[14]. Будем полагать, что температура газа в роторе Т=const и выходящие потоки газа из него равны нулю. Известно [12], что замкнутая система, в рассматриваемом случае смесь газов, может совершать вращательное движение как целое, оставаясь в термодинамическом равновесии. Отметим, что возникновение внутреннего движения газа приводит к выходу его из равновесного состояния. Такого внутреннего движения газа нет, если газ вращается в цилиндре как целое с постоянной по объему угловой скоростью. При описании равновесного состояния газа его равномерное вращение можно учесть, вводя два силовых поля: поле центробежных сил и поле сил Кориолиса. Сила Кориолиса возникает при движении газа относительно системы координат, вращающейся с угловой скоростью Ω. Она пропорциональна скорости движения газа в плоскости, перпендикулярной оси вращения. Поэтому поле сил Кориолиса действует на газ лишь в неравновесном состоянии, а в состоянии термодинамического равновесия свойства вращающегося газа зависят лишь от поля центробежных сил. Для однокомпонентного газа условием термодинамического равновесия системы, находящейся в неоднородном поле сил u(r) должно быть дополнено условием на химический потенциал µ: µ + u(r) = const, (1.1) где µ = µ(p, T) – химический потенциал газа при u = 0. Отметим, что при u=0 и T=const это условие сводится к условию постоянства в равновесии давления в объеме газа. В случае вращающегося в цилиндре газа поле центробежных сил
и соотношение (1.1) принимает следующий вид:
где M – молярная масса газа. Для дифференциала химического потенциала имеет место следующее термодинамическое соотношение: dµ = −sdT + V dp, (1.3) где s и V – энтропия и объем, отнесенные к одному молю. При температуре газа в цилиндре T=const из (1.2) и (1.3) следует: V dp = или
Равенство (1.4, 1.5) означает, что сила, равная градиенту давления в радиальном направлении, уравновешивается центробежной силой, действующей на единичный объем массой ρ =Mp/RT. Используя уравнение состояния идеального газа p =ρ RT/M, получим:
Интегрирование (1.6) дает распределение давления газа по радиусу во вращающемся цилиндре при условии постоянства температуры газа T: p(r) = p(0) exp (
Рис.1. Зависимость давления гексофторида урана
Здесь p(0) – давление газа на оси цилиндра, R – универсальная газовая постоянная, A = Физический смысл уравнения (1.2) и распределения (1.7) можно пояснить следующим образом. Молекулы газа под воздействием центробежной силы движутся по радиусу от оси к стенке ротора. Но хаотичное тепловое движение молекул стремится восстановить в объеме ротора равномерную плотность газа. Вследствие этого при постоянной температуре и в отсутствие других движений газа внутри ротора устанавливается термодинамическое распределение Больцмана в поле центробежных сил. Давление (и плотность газа) возрастает по радиусу от минимального значения на оси до максимального возле стенки ротора согласно известной барометрической формуле. Таким образом, условие (1.2) на химический потенциал в пространственно-неоднородном поле центробежных сил приводит к сильной экспоненциальной зависимости давления от радиальной координаты.
|

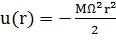 ,
, , (1.2)
, (1.2) , (1.4)
, (1.4) . (1.5)
. (1.5)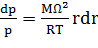 , (1.6)
, (1.6)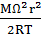 ) = p(0) exp
) = p(0) exp  . (1.7)
. (1.7)
 от радиальной координаты во вращающемся с постоянной угловой скоростью
от радиальной координаты во вращающемся с постоянной угловой скоростью цилиндре радиуса
цилиндре радиуса  = 0,065 м
= 0,065 м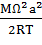 . Константа А характеризует отношение кинетической энергии вращения газа к его тепловой энергии.
. Константа А характеризует отношение кинетической энергии вращения газа к его тепловой энергии.


