Теоретический анализ. Получим аналитическое выражение для декремента затухания волн, поляризованных вдоль оси вращения в центробежном поле сил
Получим аналитическое выражение для декремента затухания волн, поляризованных вдоль оси вращения в центробежном поле сил. Для этого запишем систему уравнений для аксиальной компоненты скорости в цилиндрической системе координатах:
Подставляя выражение
Решение уравнения (2.10) будет состоять из общего однородного и частного неоднородного:
Решая общее однородное уравнение
получим:
Решая частное неоднородное уравнение
получим:
Их сумма запишется как:
Усредняя, получаем:
Так как энергия пропорциональна квадрату скорости, окончательно получим:
где
Так как вторая вязкость не внесёт значительного вклада, а теплопроводность на этом этапе не учитывается, запишем формулу (1.24) без второй вязкости и теплопроводности:
Запишем коэффициент поглощения звуковых волн в единицу времени:
Принимая во внимание то, что k=ω/c и перейдя к единым обозначениям получим выражение для распределения энергии:
где которое принимает вид резонансной кривой. Теперь перейдем к выводу коэффициента затухания звука в центробежном поле сил. Для этого запишем общий вид коэффициента затухания звука в трубе без вращения [10]:
где
Для вращающейся системы:
где Следовательно, коэффициент затухания звуковых волн в центробежном поле сил будет равен:
После преобразований, получаем следующую формулу для коэффициента затухания звуковых волн в центробежном поле сил выраженную через коэффициент затухания звуковых волн в покоящейся трубе:
|
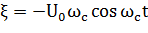, и решая систему получим следующее уравнение:
. (2.10)
.
,
.
.
.
,
- нормировочная постоянная.
, 
, а 
– нормировочная постоянная,
.
,
.
,
. (2.11)
