Верификация
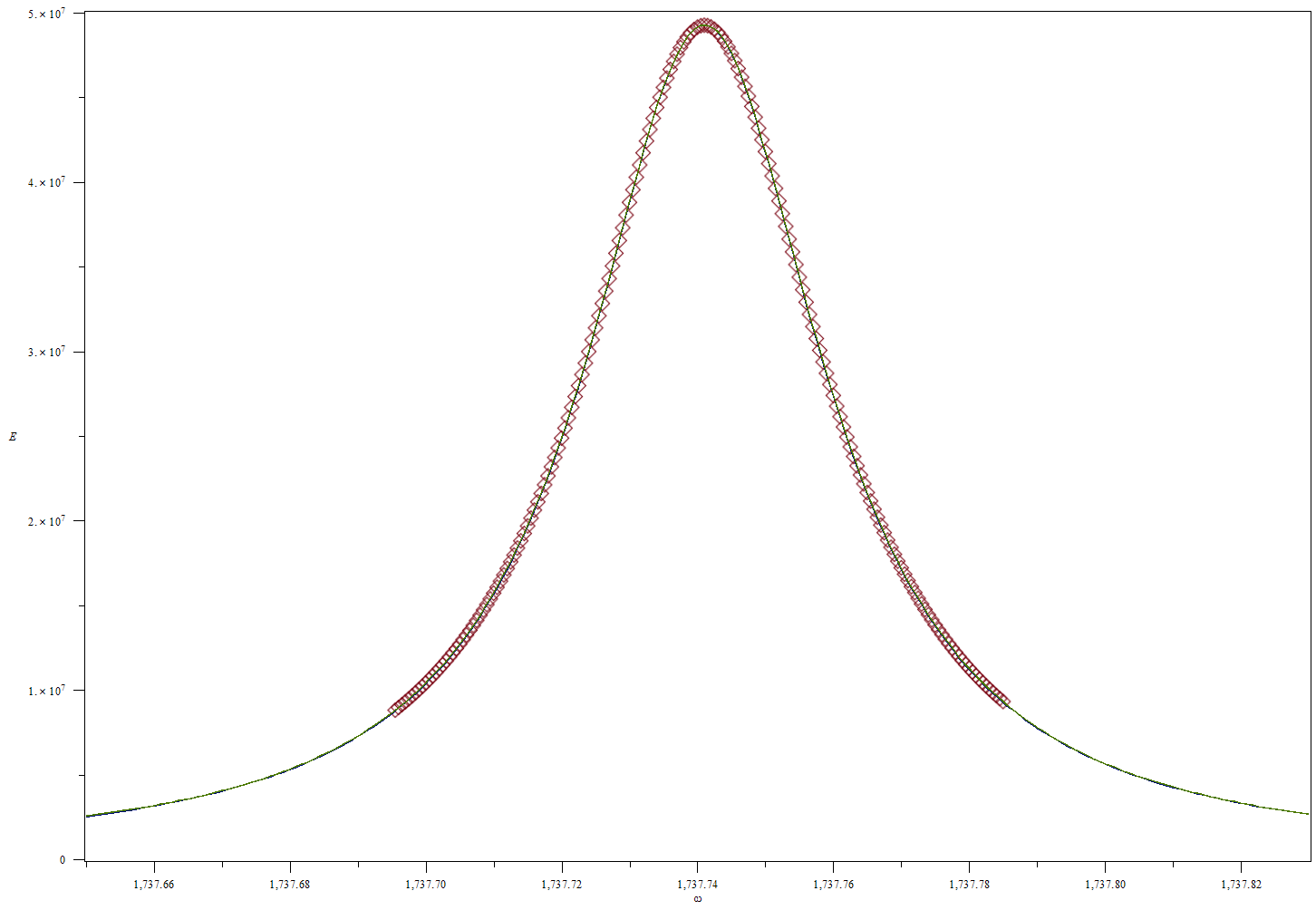
Верификацию данной программы начнём с рассмотрения покоящегося цилиндра без трения на стенках заполненного вязким газом. Для этого положим скорость вращения равную нулю и теплопроводность близкую к нулю (теплопроводность в программе нельзя задать нулевой, иначе уравнения вырождаются и Maple не понимает, как считать систему) и используем граничные условия свободного скольжения на стенках. Построив теоретический график зависимости энергии волны от ее частоты, и сравнив его с полученным численно (Рис.8), легко увидеть, что на данном этапе метод даёт правильный результат.
Рис.8. Графики зависимости энергии волны от её частоты в вязком газе. Кривая зеленого цвета – теоретическая кривая, кривая синего цвета получена интерполяцией расчетных значений. Ниже представлены теоретическая и аппроксимированная функции для данного случая, соответственно:
Среднеквадратичное отклонение коэффициента затухания, рассчитанного по этому методу от теоретического, составляет 0,76%. Далее рассмотрим покоящийся цилиндр без трения на стенках заполненный вязким теплопроводящим газом, и сравним результаты с теоретическими (Рис.9).
Рис.9. Графики зависимости энергии волны от её частоты в вязком теплопроводящем газе. Кривая зеленого цвета – теоретическая кривая, кривая синего цвета получена интерполяцией расчетных значений.
Здесь представлены теоретическая и аппроксимируемая резонансные кривые для данного случая, соответственно:
Среднеквадратичное отклонение коэффициента затухания, рассчитанного по этому методу от теоретического, составляет 0,78%. Как видно из Рис.8 и Рис.9 теоретическая и рассчитанная резонансные кривые совпадают, это говорит о правильности расчетов. Получим теперь численно зависимости коэффициента затухания звуковых волн в газе для двух случаев, имеющих теоретическое решение. Первый случай - это покоящийся цилиндр, заполненный вязким теплопроводящим газом. Трение о стенку ротора для рассматриваемого случая не учитываем. Ранее для этого случая была получена формула (1.24): считаем, что член со второй вязкостью
Для наглядности преобразуем (2.9) в зависимость глубины проникновения звуковой волны от её волнового числа:
На Рис.10 представлены теоретический и расчетный графики зависимости длины затухания волны от ее волнового числа в вязком теплопроводящем газе.
Рис.10. Графики зависимости длины затухания волны от её волнового числа построенные с учётом вязкости и теплопроводности в логарифмическом масштабе.
Видно, что зависимость имеет степенной характер. Более того среднеквадратичное отклонение расчетной зависимости от теоретической оказывается даже меньше, чем для резонансной кривой и составляет 0,52%. Рассмотрим второй случай - покоящийся цилиндр с трением на стенках заполненный идеальным газом. Теоретическая зависимость коэффициента поглощения от частоты возмущения имеет вид [10]:
также преобразуем её в зависимость глубины проникновения звуковой волны от её волнового числа:
На Рис.11 представлены теоретический и расчетный графики для рассматриваемого случая.
Рис.11. Графики зависимости длины затухания волны от её волнового числа построенные с учётом трения на внешней стенке в логарифмическом масштабе.
Эти графики также совпадают. А среднеквадратичное отклонение для этого случая составляет 0,56%. Предполагая, что коэффициент затухания аддитивная величина. И зная, что формула (2.13) учитывает только поглощение за счёт вязкости и теплопроводности, а формула (2.14) учитывает поглощение за счёт трения о стенку, производим расчет, учитывающий оба этих явления. И сравниваем результат с теоретическими предсказаниями, которые складываются из первого и второго эффекта по формуле:
на Рис.12 видно, что теоретическая и расчетная зависимости имеют одинаковый вид.
Рис.12. Графики зависимости длины затухания волны от её волнового числа построенные в логарифмическом масштабе.
Как теоретическая, так и расчетная зависимости при малых волновых числах k асимптотически стремятся к зависимости, учитывающей трение о стенку, а при больших волновых числах k учитывающую вязкость. Отсюда можно сделать вывод, что при малых волновых числах k основную роль в затухании играет процесс трения на стенках, но при их росте всё большую роль играет вязкость газа и его теплопроводность. 2.5. Расчёт Теперь рассчитаем случай максимально приближенный к реальной центрифуге: вращающийся цилиндр со всеми диссипативными взаимодействиями (трением на внешней стенке, вязкостью и теплопроводностью). Для этого случая теоретических зависимостей нет, поэтому нам придётся полагаться на расчет и полученный ранее коэффициент затухания звука в центробежном поле сил. Зная зависимость коэффициента затухания звука от его частоты (1.24) и рассчитанный выше поправочный коэффициент на скорость вращения ротора (2.8), несложно получить зависимость длины затухания волны от её волнового числа для рассматриваемого случая:
с которой расчёт полностью согласуется. Формула (2.14) не учитывает трения на стенках цилиндра. На данный момент не существует теоретических моделей, учитывающих трение на стенках цилиндра для звуковых волн в сильном центробежном поле. Поэтому для этого случая построен численный график зависимости длины затухания звуковой волны от ее волнового числа. Производя вычисления по формуле:
Где получаем зависимость глубины проникновения волны от ее волнового числа, учитывающую молекулярную вязкость, теплопроводность и трение на стенке ротора. Все зависимости приведены на Рис.13.
Рис.13. Графики зависимости глубины проникновения волны от её волнового числа построенные в логарифмическом масштабе.
С помощью Рис.12 и Рис.13 можно сделать вывод о характере затухания звуковой волны в центробежном поле. При малых волновых числах k основную роль в затухании играет процесс трения на стенках, и так же, как и без поля, с ростом увеличивается роль объемных процессов диссипации. Зависимости имеют идентичный вид, однако смещенный по оси примерно на два порядка. Это говорит о том, что дополнительным параметром диссипации является центробежное поле сил. Также проведён расчет зависимости длины пробега звуковой волны в вязком теплопроводящем газе от радиуса ротора для двух случаев: с трением и без. Результаты расчета представлены на Рис.14.
Рис.14. Графики зависимости длины затухания волны от радиуса ротора в вязком теплопроводящем газе для двух случаев: Посмотрев на Рис.15 можно видеть, что, когда рассматривается случай без трения о стенку длина затухания волны растет прямо пропорционально радиусу ротора. Это понятно если провести аналогию с током, текущим по проводу: чем больше площадь сечения провода, тем больше его проводимость. Но если рассматривать случай с трением о стенку ротора, то зависимость имеет вид ассиметричного колокола. С пиком в области 2 см. Этот пик можно объяснить следующим образом. Сила трения о стенку ротора увеличивается пропорционально радиусу ротора. При значениях радиуса близких к нулю влияние силы трения незаметно. Начиная со значения радиуса равного примерно 0,5 см сила трения начинает воздействовать на волну, тем самым заставляя ее затухать. А так как сила увеличивается прямо пропорционально радиусу, то в какой-то момент возникает пик.
|






 не внесёт существенной поправки:
не внесёт существенной поправки: , (2.12)
, (2.12) (2.13)
(2.13)
 – экспериментальный график,
– экспериментальный график,  – теоретический график
– теоретический график
 (2.14)
(2.14)
 – экспериментальный график,
– экспериментальный график,  – теоретический график
– теоретический график (2.15)
(2.15)
 - экспериментальный график учитывающий вязкость, теплопроводность и трение на внешней стенке,
- экспериментальный график учитывающий вязкость, теплопроводность и трение на внешней стенке,  - теоретический график учитывающий вязкость и теплопроводность,
- теоретический график учитывающий вязкость и теплопроводность,  - теоретический график учитывающий трение на внешней стенке,
- теоретический график учитывающий трение на внешней стенке,  - теоретическая зависимость рассчитанная по формуле (2.15)
- теоретическая зависимость рассчитанная по формуле (2.15) =
= 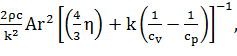 (2.16)
(2.16) (2.17)
(2.17) - расчетная зависимость глубины проникновения волны от ее волнового числа с учетом силы трения,
- расчетная зависимость глубины проникновения волны от ее волнового числа с учетом силы трения,
 глубины проникновения учитывающая вязкость, теплопроводность и трение на внешней стенке рассчитанная экспериментально,
глубины проникновения учитывающая вязкость, теплопроводность и трение на внешней стенке рассчитанная экспериментально,  теоретическая зависимость, рассчитанная по формуле (2.17)
теоретическая зависимость, рассчитанная по формуле (2.17)
 - с трением,
- с трением,  - без трения
- без трения


