Затухание звуковых волн
Одной из главных причин затухания звуковых волн в газе, является наличие вязкости и теплопроводности, приводящее к диссипации энергии звуковых волн, в связи с чем звук поглощается, т.е. его интенсивность постепенно уменьшается. Выведем формулу, использующуюся в данной работе для расчета коэффициента затухания звука, учитывающую диссипацию энергии за счет молекулярной вязкости и теплопроводности. Для вычисления диссипируемой в единицу времени энергии Емех воспользуемся следующими общими соображениями. Механическая энергия представляет собой не что иное, как максимальную работу, которую можно получить при переходе из данного неравновесного состояния в состояние термодинамического равновесия. Как известно из термодинамики, максимальная работа совершается, если переход происходит обратным образом (т.е. без изменения энтропии), и равна соответственно этому: Емех = Е0-Е(S), Где Е0 есть заданное начальное значение энергии тела в состоянии равновесия с той же энтропией S, которую тело имело вначале. Дифференцируя по времени, получаем: Емех = - Е(S) = - Производная от энергии по энтропии есть температура. Поэтому
Емех = Т0 S. Воспользуемся для S выражением:
включающим в себя возрастание энтропии, обусловленное как теплопроводностью, так и вязкостью. Поскольку температура Т мало меняется вдоль жидкости и мало отличается от Т0, то можно вынести ее из-под знака интеграла и писать Т вместо Т0:
Эта формула представляет собой обобщение формулы
на случай сжимаемой жидкости и наличия теплопроводности. Пусть ось х совпадает с направлением распространения звуковой волны. Тогда
Два последних члена в (1.21) дают
Нас, конечно, интересует среднее по времени значение величин; усреднение дает
(V0 – объем жидкости). Далее, вычислим первый член в (1.21). Отклонение Т′ температуры в звуковой волне от своего равновесного значения связано со скоростью формулой
так что градиент температуры равен
Для среднего по времени значения от первого члена в (1.21) получаем:
С помощью известных термодинамических формул
можно переписать выражение в виде
Собирая полученные выражения, находим среднее значение диссипации энергии в виде
Полная же энергия звуковой волны равна
Для звука имеем дело с задачей, в которой звуковая волна распространяется вдоль жидкости и ее интенсивность падает с увеличением пройденного расстояния x. Очевидно, что это уменьшение будет происходить по закону
Подставляем сюда (1.22) и (1.23), находим, таким образом, следующее выражение для коэффициента поглощения звука[10]:
которое используется для расчёта объёмного эффекта затухания звуковых волн при верификации.
|

 S.
S. (1.21)
(1.21)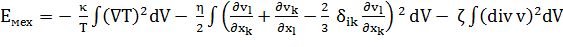 .
.

 .
. .
.
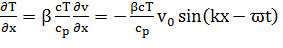 .
. .
.
 .
. (1.22)
(1.22)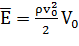 . (1.23)
. (1.23) , а для амплитуды как –
, а для амплитуды как –  , где коэффициент поглощения γ определяется посредством
, где коэффициент поглощения γ определяется посредством .
. , (1.24)
, (1.24)


