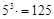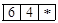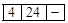Дмитрий Байда, Елена Любимова. Нехай Т — бінарне дерево, — його корінь, і — його ліве й праве піддерева:
Нехай Т — бінарне дерево,
Для заданого дерева можна визначити такі впорядковані обходи: — згори вниз (ще кажуть: у прямому порядку): — зліва направо (ще кажуть: у внутрішньому порядку): — знизу вгору (ще кажуть: у зворотному порядку): У свою чергу піддерева Приклад. Для заданого бінарного дерева запишемо послідовності вершин, які визначають різні обходи:
Для довільних k -арних дерев також можна вказати узагальнені порядки обходу:
При аналізі різноманітних арифметичних і логічних виразів можна застосовувати дерева і їхній обхід. Приклад. Нехай дано арифметичний вираз
Здійснимо обхід дерева, використовуючи всі три способи. При обході дерева згори вниз одержимо польський (префіксний) запис початкового виразу:
При обході зліва направо матимемо інфіксний запис:
Цей запис не містить дужок, потрібних для визначення порядку виконання операцій, і тому він сприймається неоднозначно. Якщо ж, відповідно до обходу дерева зліва направо, кожну операцію з аргументом взяти в дужки, то одержимо запис При обході дерева знизу вгору матимемо зворотний польський (постфіксний) запис:
Із наведеного прикладу видно, що в усіх трьох формах подання арифметичного виразу порядок аргументів (тобто листків дерева) зберігається тим самим; змінюється лише порядок знаків операцій. У програмуванні використовують польські записи — префіксний і постфіксний, які є однозначними. У програмуванні використовують польські записи — префіксний і постфіксний, які є однозначними. Для обчислення значення виразу, поданого польським (префіксним) записом, його проглядають справа наліво (тобто з кінця на початок) і виділяють два операнди разом зі знаком операції перед ними. Ці операнди і знак операції вилучають зі списку, виконують операцію і результат записують на місце вилучених символів. Приклад. Арифметичному виразові
Для обчислення значення виразу, поданого зворотним польським (постфіксним) записом, його проглядають зліва направо (тобто з початку на кінець) і виділяють два операнди разом зі знаком операції після них. Ці операнди і знак операції вилучають зі списку, виконують операцію і результат записують на місце вилучених символів. Приклад. Арифметичному виразові
[1] Кірхгоф Густав Роберт (Kirchhoff Gustav Robert, 1824 – 1887) — німецький фізик і механік. [2] Цю формулу було одержано К. Борхардтом 1860 року як побічний результат обчислення визначника, а Келі в 1889 році дав незалежне досить розпливчасте виведення цієї формули. [3] (J Kruskal;) Дмитрий Байда, Елена Любимова Библейские картинки,
|

 — його корінь,
— його корінь,  і
і  — його ліве й праве піддерева:
— його ліве й праве піддерева: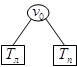
 ;
;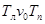 ;
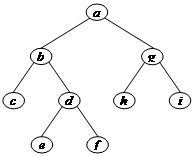
;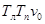 .
.
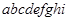 — згори вниз;
— згори вниз;  — зліва направо;
— зліва направо; 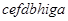 — знизу вгору.
— знизу вгору.
 — згори вниз;
— згори вниз;  — зліва направо;
— зліва направо;  — знизу вгору.
— знизу вгору. . Цьому виразові відповідає таке бінарне дерево (на дереві операцію множення позначено *, а піднесення до степеня — ^):
. Цьому виразові відповідає таке бінарне дерево (на дереві операцію множення позначено *, а піднесення до степеня — ^):
 .
. .
. , який сильно нагадує початковий вираз
, який сильно нагадує початковий вираз  .
. , значення якого дорівнює –15, відповідає польський (префіксний) запис
, значення якого дорівнює –15, відповідає польський (префіксний) запис  . Покрокове обчислення значення виразу за його польським записом виконаємо в таблиці:
. Покрокове обчислення значення виразу за його польським записом виконаємо в таблиці: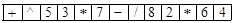





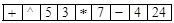
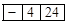


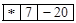

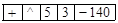






 . Покрокове обчислення значення виразу за його зворотним польським записом виконаємо в таблиці:
. Покрокове обчислення значення виразу за його зворотним польським записом виконаємо в таблиці: