Условие генерации лазера
Лазер представляет собой; как известно, систему из двух обращенных друг к другу зеркал, образующих открытый оптический резонатор, между которыми располагается активное вещество, обеспеченное системой подвода энергии (системой накачки). В резонаторе лазера могут существовать стоячие электромагнитные волны, подобно тому, как существуют стоячие волны механических деформаций в струне, зажатой с двух концов. Условие образования стоячих волн одно и то же в обоих случаях: на длине L резонатора (струны) должно укладываться целое число q полуволн
Учитывая, что для световых волн
Если каким-либо образом возбудить стоячие волны в пустом генераторе, то они очень быстро затухнут, поскольку создать идеально отражающие зеркала нельзя, и при каждом отражении от зеркал часть световой энергии теряется. Если поместить между зеркалами активную среду с достаточно большим усилением, то можно скомпенсировать потери энергии на зеркалах и получить в резонаторе незатухающие стоячие электромагнитные волны. Сделав одно из зеркал полупрозрачным и увеличив соответственно усиление среды можно вывести наружу часть излучения, существующего в резонаторе. Это и будет лазерное излучение. Лазерная генерация осуществляется на частотах
К точке I волна подойдет усиленной; в соответствии с (21) ее интенсивность будет равна
После отражения от зеркала З2 интенсивность принимает значение I2=r1I1. К точке З отраженная волна подойдет с интенсивностью
После отражения от зеркала ЗI интенсивность равна I0=r1I3; в точке “x” интенсивность этой волны достигает величины
Для возникновения генерации необходимо, чтобы интенсивность
Выразив
При выводе (28) мы для простоты пренебрегли потерями света в активной среде, а также дифракционными потерями энергии на зеркалах. Из формул (28), (21), (18) видно, что коэффициент Эйнштейна А21 (или обратная ему величина
|

 :
: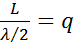 (23)
(23)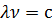 из (22) легко получить формулу для собственных частот резонатора:
из (22) легко получить формулу для собственных частот резонатора: (24)
(24)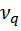 (24), располагающихся в непосредственной окрестности центральной частоты
(24), располагающихся в непосредственной окрестности центральной частоты 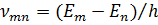 инвертированного перехода, точнее вблизи вершины контура спектральной линии, где усиление достаточно велико (см. рис.8). В типичных условиях интервал
инвертированного перехода, точнее вблизи вершины контура спектральной линии, где усиление достаточно велико (см. рис.8). В типичных условиях интервал  между собственными частотами резонатора составляет около 108 Гц, так что обычно
между собственными частотами резонатора составляет около 108 Гц, так что обычно  и генерация возможна сразу на нескольких близких собственных частотах резонатора.
и генерация возможна сразу на нескольких близких собственных частотах резонатора.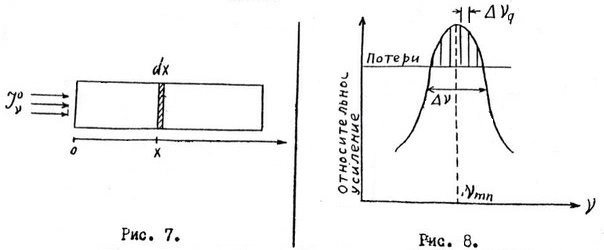
 Но насколько большим должно быть усиление активной среды для того, чтобы возникла лазерная генерация? Ответ на этот вопрос можно получить из следующих соображений (рис. 9). Пусть для простоты активная среда заполняет весь объем между зеркалами резонатора. Коэффициенты отражения зеркал З1 и З2 равны соответственно r1 и r2. (коэффициент отражения сеть отношение интенсивности отраженной световой волны, падающей на зеркало). В лазере между зеркалами резонатора распространяются две световые волны, бегущие в противоположных направлениях. На рис. 9 они для наглядности показаны разнесенными стрелками, хотя реально они распространяются в одной и той же области активной среды. Выделим в среде произвольную точку на расстоянии “х” от начала отсчета. Обозначим интенсивность волны, распространяющейся из этой точки слева направо, через Ix. Проследим, каким образом эта интенсивность будет изменяться в процессе распространения волны между зеркалами.
Но насколько большим должно быть усиление активной среды для того, чтобы возникла лазерная генерация? Ответ на этот вопрос можно получить из следующих соображений (рис. 9). Пусть для простоты активная среда заполняет весь объем между зеркалами резонатора. Коэффициенты отражения зеркал З1 и З2 равны соответственно r1 и r2. (коэффициент отражения сеть отношение интенсивности отраженной световой волны, падающей на зеркало). В лазере между зеркалами резонатора распространяются две световые волны, бегущие в противоположных направлениях. На рис. 9 они для наглядности показаны разнесенными стрелками, хотя реально они распространяются в одной и той же области активной среды. Выделим в среде произвольную точку на расстоянии “х” от начала отсчета. Обозначим интенсивность волны, распространяющейся из этой точки слева направо, через Ix. Проследим, каким образом эта интенсивность будет изменяться в процессе распространения волны между зеркалами.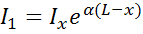 (25)
(25)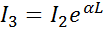 (26)
(26)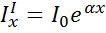 (27)
(27)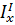 волны, пришедшей в точку “х” после двукратного прохода, была не меньше, че интенсивность Ix волны, вышедшей из этой точки, т.е.
волны, пришедшей в точку “х” после двукратного прохода, была не меньше, че интенсивность Ix волны, вышедшей из этой точки, т.е.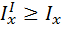
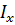 с помощью (25)-(27) получаем условие лазерной генерации:
с помощью (25)-(27) получаем условие лазерной генерации: (28)
(28)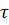 сп=1/А21) является одной из важнейших характеристик активной среды, без которой невозможен расчет лазера.
сп=1/А21) является одной из важнейших характеристик активной среды, без которой невозможен расчет лазера.


