Расчетная часть. 1. Исходя из известного временного масштаба снятой осциллограммы,1. Исходя из известного временного масштаба снятой осциллограммы, определить коэффициент Эйнштейна А21 по отношению амплитуд и сигнала спонтанного излучения в различные моменты времени. 2. Полагая, что измеренная величина А21, характеризует линию R1 (рис.10) рассчитать коэффициенты Эйнштейна В12, В21 (13), а также поперечное сечение процесса вынужденного излучения Поскольку показатель преломления рубина n=1,76, в соответствующих формулах следует всюду заменить скорость света “с” на величину с/n. 3. Располагая значением пороговое значение плотности инверсной населенности
для рубинового лазера длиной L=10 см c коэффициентами отражения зеркал r1=1 и r2=0,5. 4. Для порогового уровня инверсной населенности населения рассчитать значения плотностей населенностей N(E),N(2
где N –концентрация атомов; положить N=2 Кроме того, учесть, чтов силу закона Больцмана 5. Оценить по формуле
минимальную объемную плотность энергии возбуждения, необходимую длядостижения инверсной населенности в импульсном режиме. (
ЛИТЕРАТУРА 1. Микаэлян А.Л., Тер –Микаэлян М.Л., Турков Ю.Г. Оптические генераторы на твѐрдом теле, М «Сов. Радио» 1967. 2. А. Ярив, Квантовая электроника и нелинейная оптика, М. «Сов. Радио», 1973
|
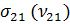(19). В расчетах положить 
4.3 
1014 Гц.
),N(4А2),при этом учесть, что
при комнатной температуре.
) в лазере с вышеприведенными данными.
