Идея метода Ритца заключается в том, что значение некоторого функционала  рассматривается не на произвольных допустимых кривых данной вариационной задачи, а лишь на всевозможных линейных комбинациях
рассматривается не на произвольных допустимых кривых данной вариационной задачи, а лишь на всевозможных линейных комбинациях

с постоянными коэфициентами составленных из n первых функций некоторой выбранной последовательности функций
 (2. 2)
(2. 2)
Функции (2.1) должны быть допустимыми в рассматриваемой задаче, что налагает некоторые ограничения на выбор последовательности функций 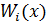 . На таких линейных комбинациях функционал
. На таких линейных комбинациях функционал  превращается в функцию
превращается в функцию 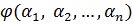 коэффициентов
коэффициентов  . Эти коэффициенты
. Эти коэффициенты  выбираются так, чтобы функция
выбираются так, чтобы функция 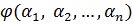 достигала экстремума; следовательно,
достигала экстремума; следовательно,  должны быть определены из системы уравнений
должны быть определены из системы уравнений

Совершая предельный переход при  , получим в случае существования предела функцию
, получим в случае существования предела функцию
 являющуюся (при некоторых ограничениях, налагаемых на функционал
являющуюся (при некоторых ограничениях, налагаемых на функционал  и на последовательность
и на последовательность  точным решением рассматриваемой вариационной задачи. Если не совершать предельного перехода, а ограничится лишь
точным решением рассматриваемой вариационной задачи. Если не совершать предельного перехода, а ограничится лишь  первыми членами
первыми членами
 то получим приближенное решение вариационной задачи.
то получим приближенное решение вариационной задачи.
Если таким методом определяется абсолютный минимум функционала, то приближенное значение минимума функционала находится с избытком, так как минимум функционала на любых допустимых кривых не больше, чем минимум того же функционала на части этого класса допустимых кривых – на кривых вида
 При нахождении тем же методом максимального значения функционала получаем по тем же причинам приближенное значение максимума функционала с недостатком.
При нахождении тем же методом максимального значения функционала получаем по тем же причинам приближенное значение максимума функционала с недостатком.
Для того чтобы функции  были допустимыми, прежде всего необходимо удовлетворять граничным условиям. Если граничные условия линейны и однородны, например, в простейшей задаче
были допустимыми, прежде всего необходимо удовлетворять граничным условиям. Если граничные условия линейны и однородны, например, в простейшей задаче  или
или

где  - постоянные, то проще всего и координатные функции выбрать удовлетворяющими этим граничным условиям. Очевидно, что при этом и
- постоянные, то проще всего и координатные функции выбрать удовлетворяющими этим граничным условиям. Очевидно, что при этом и  при любых
при любых  будут удовлетворять тем же граничным условиям. Пусть, например, граничные условия имеют вид
будут удовлетворять тем же граничным условиям. Пусть, например, граничные условия имеют вид

Тогда в качестве координатных функций можно выбрать

Где  - какие-нибудь непрерывные функции, или
- какие-нибудь непрерывные функции, или

или какие-нибудь другие функции, удовлетворяющие условиям

Если условия неординарны, например
 где хотя бы одно из чисел
где хотя бы одно из чисел  отлично от нуля, то проще всего искать решение вариационной задачи в виде
отлично от нуля, то проще всего искать решение вариационной задачи в виде

Где  удовлетворяет заданным граничным условиям
удовлетворяет заданным граничным условиям 
 , а все остальные
, а все остальные 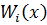 удовлетворяют соответствующим однородным граничным условиям, т. е. в рассматриваемом случае
удовлетворяют соответствующим однородным граничным условиям, т. е. в рассматриваемом случае  Очевидно, что при таком выборе при любых
Очевидно, что при таком выборе при любых  функции
функции  удовлетворяет заданным граничным условия. В качестве функции
удовлетворяет заданным граничным условия. В качестве функции  можно выбрать, например, линейную функцию
можно выбрать, например, линейную функцию

Решение системы уравнений

вообще говоря, является весьма сложной задачей. Эта задача значительно упрощается, если на экстремум исследуется квадратичный относительно неизвестной функции и ее производных функционал  , так как в этом случае уравнения (2. 7) линейны относительно
, так как в этом случае уравнения (2. 7) линейны относительно  .
.
Выбор последовательности функций  , называемых координатными функциями, сильно влияет на степень сложности дальнейших вычислений, и поэтому от удачного выбора координатной системы функций в значительной мере зависит успех применения этого метода.
, называемых координатными функциями, сильно влияет на степень сложности дальнейших вычислений, и поэтому от удачного выбора координатной системы функций в значительной мере зависит успех применения этого метода.
ЗАДАЧИ

 рассматривается не на произвольных допустимых кривых данной вариационной задачи, а лишь на всевозможных линейных комбинациях
рассматривается не на произвольных допустимых кривых данной вариационной задачи, а лишь на всевозможных линейных комбинациях
 (2. 2)
(2. 2)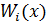 . На таких линейных комбинациях функционал
. На таких линейных комбинациях функционал 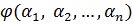 коэффициентов
коэффициентов  . Эти коэффициенты
. Эти коэффициенты 
 , получим в случае существования предела функцию
, получим в случае существования предела функцию являющуюся (при некоторых ограничениях, налагаемых на функционал
являющуюся (при некоторых ограничениях, налагаемых на функционал  первыми членами
первыми членами то получим приближенное решение вариационной задачи.
то получим приближенное решение вариационной задачи. При нахождении тем же методом максимального значения функционала получаем по тем же причинам приближенное значение максимума функционала с недостатком.
При нахождении тем же методом максимального значения функционала получаем по тем же причинам приближенное значение максимума функционала с недостатком. были допустимыми, прежде всего необходимо удовлетворять граничным условиям. Если граничные условия линейны и однородны, например, в простейшей задаче
были допустимыми, прежде всего необходимо удовлетворять граничным условиям. Если граничные условия линейны и однородны, например, в простейшей задаче  или
или
 - постоянные, то проще всего и координатные функции выбрать удовлетворяющими этим граничным условиям. Очевидно, что при этом и
- постоянные, то проще всего и координатные функции выбрать удовлетворяющими этим граничным условиям. Очевидно, что при этом и  при любых
при любых  будут удовлетворять тем же граничным условиям. Пусть, например, граничные условия имеют вид
будут удовлетворять тем же граничным условиям. Пусть, например, граничные условия имеют вид
 - какие-нибудь непрерывные функции, или
- какие-нибудь непрерывные функции, или

 где хотя бы одно из чисел
где хотя бы одно из чисел  отлично от нуля, то проще всего искать решение вариационной задачи в виде
отлично от нуля, то проще всего искать решение вариационной задачи в виде
 удовлетворяет заданным граничным условиям
удовлетворяет заданным граничным условиям 
 , а все остальные
, а все остальные 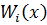 удовлетворяют соответствующим однородным граничным условиям, т. е. в рассматриваемом случае
удовлетворяют соответствующим однородным граничным условиям, т. е. в рассматриваемом случае  удовлетворяет заданным граничным условия. В качестве функции
удовлетворяет заданным граничным условия. В качестве функции  можно выбрать, например, линейную функцию
можно выбрать, например, линейную функцию

 , так как в этом случае уравнения (2. 7) линейны относительно
, так как в этом случае уравнения (2. 7) линейны относительно 


