Метод ветвей и границ. Общая схема
Метод ветвей и границ представляет собой комбинаторный метод, т.е. упорядоченный перебор вариантов и рассмотрение лишь тех из них, которые по некоторым признакам оказываются перспективными. Он имеет достаточно широкую сферу применения, поэтому рассмотрим его общую схему. Пусть существует некоторая функция f(X), экстремум которой (например, максимум) необходимо найти при некоторой системе ограничений. Этой системой определяется ОДП задачи - обозначим ее G. Пусть некоторым способом мы можем определить верхнюю границу функции на этой области Затем проверяют, не существует ли какой-нибудь очевидный способ нахождения точки X0, для которой f(X0)= Если такого способа нет, то множество G разбивают на подмножества G1 и G2 и для каждого из них находят верхнюю границу
Этот процесс может быть изображен в виде дерева (рис.18). На каждом шаге процесса делается попытка найти точку Х в соответствующем подмножестве, на которой реализуется его верхняя граница. Если попытка не удается, то ветвление продолжают, рассматривая каждый раз наиболее перспективное подмножество (для его выбора сравнивают оценки вершин дерева, из которых нет выходов). Если попытка найти Х: f(X) = При решении задачи на минимум схема та же, но рассматриваются вершины с наименьшей оценкой. Этот метод всегда сходится, если мы имеем дело с ограниченной дискретной областью. Чтобы конкретизировать метод ветвей и границ, необходимо установить: 1) алгоритм поиска границ 2) алгоритм разбиения множества на части; 3) алгоритм поиска Х, реализующего границу 4) сходимость метода.
|

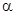 0, т.е.
0, т.е.  f(X), X
f(X), X  G.
G.



