Задача о ранце
ПРИМЕНЕНИЕ МЕТОДА ВЕТВЕЙ И ГРАНИЦ В ЗАДАЧАХ ВЫБОРА. Некоторые задачи в менеджменте это задачи принятия обоснованных управленческих решений при выборе наилучшего варианта из конечного множества возможных альтернатив. Наиболее общий метод решения таких задач это метод ветвей и границ (МВГ). Метод представляет собой последовательность действий: 1) Все множества вариантов представляется в виде дерева, конечные вершины которого соответствуют конкретным вариантам; каждая ветвь дерева отвечает подмножеству возможных вариантов. 2) На каждой ветви (подмножестве), вводится функция φ, являющаяся верхней (при поиске максимума) или нижней (при поиске минимума) границей целевой функции. Если имеется вариант решения лучший, чем значение функции на некоторой ветви дерева (подмножестве решений), то вся эта ветвь может быть отсечена, т. е. исключена из дальнейшего анализа. Эффективность этого метода зависит от того, насколько удачно построено дерево вариантов, т.е. насколько эффективно отсекаются неперспективные ветви решений, в противном случае задача сводится к перебору всех возможных альтернатив. Этот метод целесообразно применять при решении таких задач как: – Задача о ранце, – Задача унификации, – Задача коммивояжера, – Задача о замене оборудования и др. Задача о ранце Имеется ранец объем которого Пусть имеется список товаров, которые мы хотим положить в ранец
Проблема возникает только тогда, когда общий объем товаров превышает объем ранца. Эта задача о выборе наилучшего варианта загрузки ранца. Пусть Чем мы управляем в этой модели? Вектором Как мы управляем? При заполнении ранца, мы ограничены его объемом, т.е.:
Зачем решается задача? Чтобы общая полезность товаров, наполняющих ранец, была максимальной, т.е.
Эту задачу можно формулировать как задачу выбора портфеля инвестиции. В этом случае
Тогда задача, которая имеет ту же самую математическую постановку, может быть сформулирована следующим образом: Вставить инвестиционный проект таким образом, чтобы суммарная прибыль от вложений была бы максимальной. Различных вариантов в этой задаче 2N, часть вариантов недопустима, т. к. они могут нарушать ограничение по объему наполнения, это так же позволит отсекать некоторые ветви. Ветвление в этой задаче организуется следующим способом: Сначала все множество вариантов разбивается на 2 подмножества: – Берем товар в ранец, – Не берем второй товар, последующее ветвление ведется аналогично. Для каждого товара первоначально рассчитывается удельная полезность товара:
Т.е. полезность единицы объема товара, и список товаров ранжируется по убыванию этой величине, т.к. товар с большей удельной полезностью для нашей цели предпочтительней. После этого применяется метод ветвей и границ. Пример решения задачи о ранце. Объем ранца
Упорядочим таблицу, в результате получим:
|

 .
. ,
, — объем i -го товара,
— объем i -го товара, — полезность конечного товара.
— полезность конечного товара.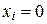 , если товар не берется в ранец, и
, если товар не берется в ранец, и  , если товар принимается.
, если товар принимается. .
.

 — объем средств для вложения в i -й проект,
— объем средств для вложения в i -й проект, — прибыль i -го инвестиционного проекта.
— прибыль i -го инвестиционного проекта.