Работа № 10 Определение коэффициента термического расширения (линейного) твердого тела
Цель работы: 1) определение температуры металлической проволоки при протекании через нее электрического тока; 2) измерение удлинения проволоки при нагревании; 3) определение показателя коэффициента термического расширения.
В работе используются: регулируемый источник постоянного тока; два цифровых вольтметра постоянного тока; теплоизолированная труба; металлическая проволока; микрометрический индикатор. Практически все физические параметры изменяются при изменении температуры тела. В данной работе экспериментально определяется коэффициент термического расширения твердого тела (металлической проволоки). Связь между температурой тела и изменением его объема задается формулой
где a - коэффициент объемного расширения, V o - объем при начальной температуре, D t - изменение температуры.
Для линейного расширения тела формула [1] приводится к виду:
где b - коэффициент линейного расширения, L o - начальная длина тела, L o = 1 м. Из формулы [2] следует, что для определения коэффициента Зависимость сопротивления металла от температуры имеет вид, аналогичный формуле [1]:
Поскольку нагрев проволоки производится протекающим через нее электрическим током, зная падение напряжения на сопротивлении и силу тока, можно вычислить сопротивление проволоки:
Силу тока определяем по падению напряжения на эталонном сопротивлении, термическим коэффициентом сопротивления которого можно пренебречь. При выполнении работы необходимо учитывать, что зависимость [2] выполняется в ограниченном интервале температур. При значительном нагреве удлинение проволоки превышает рассчитанное по формуле [2], проявляется эффект, аналогичный пластической деформации при значительном растяжении. Поэтому при обработке экспериментальных данных необходимо рассчитывать коэффициент b по температурам, незначительно отличающимся от начальной.
|

 [1]
[1]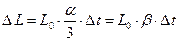 [2]
[2]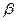 необходимо знать начальную длину проволоки L o, изменение температуры D t и соответствующее изменение длины D L. Изменение длины проволоки можно непосредственно измерить при помощи микрометрического индикатора, а температуру непосредственно измерить невозможно. Поэтому в данной работе определение температуры проволоки производится по изменению ее сопротивления при нагревании (термический коэффициент сопротивления предполагается известным).
необходимо знать начальную длину проволоки L o, изменение температуры D t и соответствующее изменение длины D L. Изменение длины проволоки можно непосредственно измерить при помощи микрометрического индикатора, а температуру непосредственно измерить невозможно. Поэтому в данной работе определение температуры проволоки производится по изменению ее сопротивления при нагревании (термический коэффициент сопротивления предполагается известным). [3]
[3] [4]
[4]


