Математические модели динамических объектов
Моделирование динамического объекта начинается с установления его типа: стационарный или нестационарный, линейный или нелинейный. Линейные стационарные объекты описываются линейными дифференциальными уравнениями с постоянными коэффициентами. Если коэффициенты линейных дифференциальных уравнений являются функциями независимых переменных, то объект относится к классу линейных нестационарных. Нелинейные стационарные объекты описываются линейными уравнениями с постоянными коэффициентами, а нелинейные нестационарные — нелинейными уравнениями с переменными коэффициентами. В изучаемом курсе рассматриваются модели линейных объектов. Аналитическое представление модели динамического объекта в виде дифференциального уравнения не является единственно возможным. Для систем автоматического регулирования принято представление модели в виде типовых линейных и нелинейных звеньев и их передаточных функций. Примером линейного стационарного динамического объекта является электрическая цепь, содержащая активные и реактивные элементы, (рисунок 1).
Рисунок 1 – Схема электрической цепи
Переходный процесс при замыкании ключа в такой цепи описывается дифференциальным уравнением
в котором i и Е являются функциями времени, а параметры цепи L и R — постоянными коэффициентами. В качестве другого примера рассмотрим движение механизма, имеющего приведенный момент инерции I и момент нагрузки Мнагр, в общем случае переменный. Механизм приводится в движение моментом двигателя М, (рисунок 2)
Рисунок 2- Расчётная схема механизма Изменение угловой скорости механизма w описывается дифференциальными уравнениями, называемыми уравнениями движения
Математическими моделями объектов в приведенных примерах являются дифференциальные уравнения первого порядка. Такие уравнения имеют семейства решений. Чтобы выбрать одно решение из многих, необходимо знать начальное значение функции, то есть ее значение в начальный момент времени. В общем виде можно записать y¢ = ¦ (y, t) y (t0) = y0. (10) Задача определения значений у для будущих значений t>t0 называется задачей Коши.
Вопросы для самопроверки 1. Какие динамические объекты относятся к линейным? 2. Какие динамические объекты относятся к стационарным? 3. Приведите математическую формулировку задачи Коши для линейного дифференциального уравнения первого порядка.? 4. Приведите примеры использования дифференциальных уравнений в профессиональной деятельности?
Численные методы решения обыкновенных дифференциальных уравнений Лишь очень немногие дифференциальные уравнения могут быть решены точно, аналитическими методами, и поэтому обычно необходимо приближать решение численными методами. Пусть требуется найти приближенное решение дифференциального уравнения y¢ = ¦ (y, t), удовлетворяющее начальному условию y (t0) = y0. Численное решение задачи состоит в нахождении значений y1, y2, …yn функции (y(t) в точках t1, t2,...tn). Точки t1, t2,...tn называют узлами сетки, а расстояние между ними — шагом. Часто решение выполняют с постоянным шагом, тогда t1 = t0 + ih, (11) где i = 1, 2,... n, h — шаг сетки. Рассмотрим два метода. Одношаговым называется метод, в котором для расчетов следующей точки требуется информация только о последней вычислительной точке. Первый из рассматриваемых методов — метод Эйлера. В методе Эйлера каждое следующее значение функции вычисляется по предыдущему по формуле: yi+1 = yi + hצ(yi, ti), i = 1, 2,... n, (12) Фрагмент программы на языке Бейсик, реализующий метод Эйлера приведен в приложении Б. Другим распространенным одношаговым методом является метод Рунге-Кутта. В этом методе величину yi+1 вычисляют по следующим формулам: yi+1 = yi + hצ(yi, ti), i = 1, 2,... n,
где k1 = ¦(yi, ti); k2 = ¦(yi + k3 = ¦(yi + k4 = ¦(yi + h k3, ti + h);
Для оценки погрешности метода часто используют правило Рунге. Для этого проводят вычисления с шагом h и c шагом h/2. Если полученные значения отличаются в пределах допустимой погрешности, то шаг удваивают, в противном случае берут половинный шаг. Фрагмент программы на языке Бейсик, реализующий метод Рунге-Кутта, приведен в приложении Б. Вопросы для самопроверки 1. Что называется сеткой и шагом метода? 2. Какие методы называются одношаговыми? 3. Приведите расчетную формулу метода Эйлера. Сколько вычислений приходится на одном шаге? 4. Приведите расчетные формулы метода Рунге-Кутта. Сколько вычислений производится на одном шаге? 5. Как оценить погрешность решения?
|


 , (8)
, (8)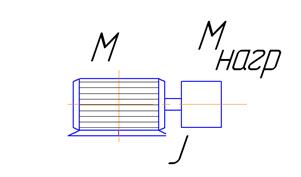

 (13)
(13) , ti +
, ti +  );
); , ti +
, ti + 


