Методы обработки экспериментальных данных
Методы оценки экспериментальных данных используют для выявления закономерностей и изучения поведения объектов. Они служат основой для построения математических моделей реальных объектов. При обработке данных в автоматике, измерительной технике, теории надежности возникает необходимость оценить характеристики случайной величины. Основными характеристиками являются математическое ожидание, дисперсия, доверительная вероятность и доверительный интервал. Часто при анализе эмпирических данных, возникает необходимость установить функциональную зависимость между величинами х и у, полученными в результате измерения. Такая задача является задачей аппроксимации. Например, функция y=f(x) задана в виде таблицы (xi, yi), i = 1, 2 … п. Требуется аппроксимировать ее многочленом заданной степени k.
где pi — коэффициенты многочлена. Для решения этой задачи широко применяется метод наименьших квадратов. Согласно этому методу коэффициенты многочлена выбирают так, чтобы сумма квадратов отклонений найденного многочлена от заданных значений функции была минимальной. Значит требуется найти такой полином Р(х), чтобы соотношение
было минимальным. Как известно из курса математического анализа, минимуму функции S соответствует нулевое значение частной производной по каждому коэффициенту. В итоге получаем систему линейных алгебраических уравнений относительно неизвестных ро, pi, pi, … рк. И решая ее, находим коэффициенты аппроксимирующего полинома.
Вопросы для самопроверки 1. Назовите основные характеристики случайной величины? 2. В чем сущность метода аппроксимации по методу наименьших квадратов?
|

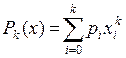 (14)
(14)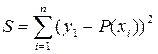 (15)
(15)


