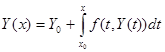Метод Пикара.

Напомним известные теоремы Пикара и Пеано о существовании и единственности решения данной задачи (задачи Коши).

Теорема ПЕАНО утверждает, что решение задачи Коши существует в некоторой окрестности точки Хо, если функция f(x,Y) непрерывна в окрестности точки (X₀,Y₀).

Теорема ПИКАРА гласит, что если не только функция f(x,Y), но и ее частная производная f'_у(x,Y) также непрерывна в окрестности точки (Х₀,У₀), то решение задачи Коши единственно на некотором отрезке, содержащем точку Х₀.

Доказательство теоремы Пикара следует из общего принципа сжимающих отображений, оно весьма непросто, но обладает существенным преимуществом -оно конструктивно. Причем последовательность функций Yn(x), которая строится в нем, сходится к решению равномерно на отрезке со скоростью геометрической прогрессии. В методе Пикара последовательность функций Yn(x) строится по рекуррентной формуле:

при n= 0,1,2,...,

а за нулевое приближение берется константа Y₀: Y₀ (х)ºY₀.

Для того, чтобы стало понятно происхождение этой рекуррентной формулы, заметим, что интегральное уравнение

эквивалентно исходной задаче Коши, поскольку любая функция Y(х), являющаяся его решением, удовлетворяет начальному условию Y(Х_о)=Y_о и уравнению Y'(х)=f(x,Y(х)) и наоборот.

Вопрос: Почему это действительно так?

Пример 4.1 Применим метод Пикара для решения уравнения Y'=Y с начальным условием Y(0)=1. Такая задача эквивалентна поиску решения интегрального уравнения Y=1+òY(t)dt.

В качестве начального приближения берем функцию Yо=1.

Тогда Y1=1+òYо(t)dt= 1+òdt= 1+x.

Далее, Y2= 1+òY1(t)dt= 1+ò(1+t)dt= 1+x+x²/2.

Y3= 1+òY2(t)dt= 1+ò(1+t+t²/2)dt= 1+x+x²/2+x³/6.

Можно убедиться, что Yn= 1+х+x²/2+ ... +xⁿ/n!.

Упражнение 4.1.Доказать последнее равенство строго, используя принцип математической индукции.

Упражнение 4.2.В примере 4.1 найти точное решение Y(Х) и оценить скорость равномерной сходимости Yn(x) -> Y(Х) на отрезке [0,1].

В целом, приближенные методы решения обыкновенных дифференциальных уравнений можно разбить на 3 типа:

· аналитические, позволяющие получить приближенное решение Y(х) в виде формулы,

· графические, дающие возможность приближенного построения графика решения Y(х),т.е. интегральной кривой,

· численные, в результате применения которых получается таблица приближенных значений функции Y(х),

хотя такое деление и несколько условно.

Кроме метода Пикара, к аналитическим методам относится и

метод разложения неизвестной функции Y(х) в ряд,

на котором мы сейчас остановимся.

Напишем формальное разложение Y(Х) в ряд Тейлора в точке а:

В это равенство входят производные неизвестной функции Y(Х) в точке а, однако именно в этой точке, пользуясь условиями задачи, мы можем последовательно найти любое число производных и получить необходимое приближение решения. В общем виде это выглядит так: Yо(а)=Y(а)= Yо; Y'(а)=f(a,Y(a))= f(a,Yo)

Дифференцируя данное нам уравнение по Х ,получим

Y''(Х)=f'_х(x,Y(х))+f'_у(x,Y(х))*Y'(х), откуда Y''(а)= f'_х(а,Yо)+f'_у(a,Yо)*f(a,Yо).

Аналогично получается и значения третьей и дальнейших производных в точке а -дифференцируем нужное число раз исходное уравнение и подставляем полученные ранее значения производных в точке а.

Пример 4.2.Выпишем первые члены разложения в ряд функции Y(x), удовлетворяющей уравнению Y'=2хY и начальному условию Y(0)=1.

Ясно, что Y(0)=1 и Y’(0)=2*0*1= 0. Далее, Y''(х)=2Y+2х*Y'(х), откуда Y''(0)=2.

Y'''(х)=2 Y'(х)+2 Y'(х)+2х*Y''(х)= 4Y'(х)+2хY''(х), откуда Y'''(0)=0.

Y⁽⁴⁾(х)=4Y''(х)+2хY'''(х), откуда Y⁽⁴⁾(0)=6.

Получаем приближенное решение Y(х)»1+х²+0.5х⁴.

Упражнение 4.3.Пользуясь формулой Лейбница для нахождения n-ой производной произведения функций, написать разложение искомой в примере 4.2 функции в ряд Тейлора.

Упражнение 4.4.Найти точное решение в примере 4.2 и оценить качество приближения в примере 4.2 на отрезке [-0.5,0.5].

Описанные выше методы не часто применяются на практике, поскольку в методе Пикара на каждом шаге приходится вычислять интеграл, что осложняет вычисления и ухудшает точность, а в методе разложения в ряд крайне сложно формализовать на любом из языков процесс нахождения производных высокого порядка, а при малом количестве членов разложения этот метод дает хорошее приближение лишь вблизи от точки а.

Среди ГРАФИЧЕСКИХ рассмотрим