Средняя арифметическая и ее свойства
Если рассматривается интервальный вариационный ряд, то средняя арифметическая, называемая взвешенной, вычисляется по формуле
Свойство 1. Если каждую варианту совокупности уменьшить или увеличить на какое-то произвольное положительное число А, то и средняя арифметическая уменьшится или увеличится на столько же. Упражнение 1. Доказать свойство 1. Свойство 2. Если каждую варианту разделить или умножить на одно и тоже число А, то и средняя арифметическая изменится во столько же раз. Упражнение 2. Доказать свойство 2. Свойство 3. Сумма произведений отклонений вариант от их средней арифметической на соответствующие им частоты равна нулю. Упражнение 3. Доказать свойство 3. Свойство 4. Сумма квадратов отклонений вариант от их средней арифметической меньше суммы квадратов отклонений тех же вариант от любой другой величины А, не равной средней арифметической. Упражнение 4. Доказать свойство 4. Размах вариации Рассмотрим еще две характеристики выборочной совокупности: дисперсию и среднее квадратическое отклонение. Эти величины характеризуют не только величину, но и специфику варьирования признака.
|

 - средняя арифметическая является центром распределения, вокруг которого группируются все варианты статистической совокупности.
- средняя арифметическая является центром распределения, вокруг которого группируются все варианты статистической совокупности.
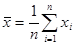 .
.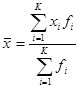 , где
, где  - частота
- частота 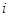 - ого класса,
- ого класса,  ,
, 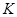 - количество классовых интервалов. Рассмотрим свойства средней арифметической.
- количество классовых интервалов. Рассмотрим свойства средней арифметической.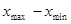 характеризует варьирование признака в совокупности.
характеризует варьирование признака в совокупности.


