Генеральная совокупность. Выборка. Статистические ряды
Пусть задача состоит в том, чтобы исследовать заданный качественный или количественный признак, характеризующий элементы некоторой последовательности (совокупности) наблюдений. Все множество объектов, входящих в рассматриваемую совокупность называют генеральной совокупностью. Число элементов генеральной совокупности может быть достаточно большим (в теоретических рассмотрениях используется и совокупности, содержащие бесконечное множество элементов). Часть генеральной совокупности, выбранную из нее некоторым (случайным) образом, называют выборочной совокупностью (выборкой). Объем выборки, обозначаемый Элементы совокупности называют вариантами. Существует два основных способа отбора вариант из генеральной совокупности: повторный и бесповторный. В практике обычно применяют бесповторный отбор. Статистическими рядами называют ряды числовых значений некоторого признака, расположенного в определенном порядке. Расположим варианты
Такую перенумерованную последовательность часто называют вариационным рядом. Числа, показывающие сколько раз отдельные варианты встречаются в данной совокупности, называются частотами или весами вариант и обозначаются Общая сумма частот всегда равна объему выборки. Говорят еще об относительных частотах (выражаются в частях или % от Интервальный вариационный ряд, такой статистический ряд, в котором частоты распределяются по отдельным интервалам или промежуткам (от - до), на которые разбивается вариация признака в пределах от минимальной до максимальной варианты совокупности. Эти промежутки или классовые интервалы могут быть равными и неравными по ширине. Чаще всего рассматриваются равные интервалы. Величина равных интервалов определяется делением размаха варьирования признака (
В общем случае техника построения вариационного ряда сводится к следующему: 1) составляем сводку исходных данных; 2) отыскиваем 3) определяем величину классового интервала 4) при построении интервального вариационного ряда следует добиваться того, чтобы минимальная варианта 5) наметив классовые интервалы, остается распределить по ним варианты выборки, то есть, определить частоты каждого класса.
|

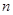 (по количеству элементов), может быть и сравнительно большим и малым, но не может содержать меньше двух единиц. Выборочный метод является основным при изучении статистических совокупностей. Его преимущество перед сплошным учетом всех членов генеральной совокупности заключается в том, что он сокращает время и затраты труда (за счет уменьшения числа наблюдений), а главное позволяет получать информацию о таких совокупностях, сплошное исследование которых практически невозможно или нецелесообразно.
(по количеству элементов), может быть и сравнительно большим и малым, но не может содержать меньше двух единиц. Выборочный метод является основным при изучении статистических совокупностей. Его преимущество перед сплошным учетом всех членов генеральной совокупности заключается в том, что он сокращает время и затраты труда (за счет уменьшения числа наблюдений), а главное позволяет получать информацию о таких совокупностях, сплошное исследование которых практически невозможно или нецелесообразно.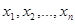 (
( , где
, где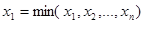 ,
,  .
.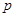 или
или  .
.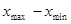 ) на число групп или классов (
) на число групп или классов (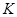 ), намечаемых при построении вариационного ряда:
), намечаемых при построении вариационного ряда: , где
, где 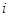 - величина классового интервала, а величина
- величина классового интервала, а величина 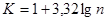 .
.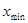 и
и 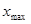 варианты;
варианты; , где
, где 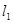 - нижняя граница первого классового интервала. Определяем верхнюю границу первого классового интервала
- нижняя граница первого классового интервала. Определяем верхнюю границу первого классового интервала 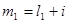 , второго классового интервала
, второго классового интервала 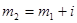 ,
, 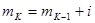 .
.


