Средние величины и показатели вариации. Вариационные ряды и их графики дают наглядное представление о том, как варьирует тот или иной количественный признак
Вариационные ряды и их графики дают наглядное представление о том, как варьирует тот или иной количественный признак. Но они недостаточны для полной характеристики статистической совокупности. Количественные показатели, которые (логически и теоретически обоснованы) позволяют судить о качественном своеобразии варьирующих объектов и сравнивать их между собой, называются статистическими характеристиками. В отличие от индивидуальных числовых характеристик средние величины обладают большей устойчивостью, способностью характеризовать группу однородных вариант одним (средним) значением. И хотя средние абстрагируют нас от конкретных вещей, они вполне понятны и ощутимы. Средний рост, средняя масса …(то есть, здесь уравновешиваются все индивидуальные отклонения и появляется качественное своеобразие группового объекта). По определению Гаусса, истинной средней служит такая величина, сумма квадратов отклонений от которой обладает нименьшим значением.
Средние величины могут характеризовать только однородную массу вариант (если это не так, следует сгруппировать варианты в отдельные качественно однородные группы и вычислять групповые средние).
Средняя геометрическая является более точной характеристикой при определении средних прибавок или при увеличении линейных размеров тел, прироста численности популяции за определенный промежуток времени.
|

 , где
, где  - средняя величина,
- средняя величина,  - варианта,
- варианта, 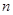 - объем выборки,
- объем выборки,  - величина, определяющая вид средней.
- величина, определяющая вид средней. - средняя гармоническая. В этом случае
- средняя гармоническая. В этом случае  . В некоторых случаях для усреднения количественных признаков используется такой тип средней.
. В некоторых случаях для усреднения количественных признаков используется такой тип средней. - средняя квадратическая. При выражении количественных признаков вариант мерами площади более точной усредненной характеристикой будет средняя квадратическая
- средняя квадратическая. При выражении количественных признаков вариант мерами площади более точной усредненной характеристикой будет средняя квадратическая 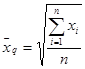 .
.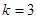 - средняя кубическая. Более точная средняя характеристика, в тех случаях, когда варьирующий признак выражен в объмных единицах.
- средняя кубическая. Более точная средняя характеристика, в тех случаях, когда варьирующий признак выражен в объмных единицах. .
. .
. - средняя арифметическая. Эту величину рассотрим подробнее.
- средняя арифметическая. Эту величину рассотрим подробнее.


