И поточечной сходимости функционального ряда
Функциональный ряд, его сумма и область сходимости Определение функционального ряда Пусть в области Δ вещественных или комплексных чисел дана последовательность функций Функциональным рядом называется сумма всех членов функциональной последовательности:
Определение области поточечной сходимости функционального ряда Множество Определение Суммы функционального ряда Функция То есть
Равномерная и поточечная сходимость Определение равномерной и поточечной сходимости функционального ряда Пусть ряд Ряд на множестве
или:
то ряд называется сходящимся поточечно (неравномерно) в Признак Вейерштрасса (достаточный признак равномерной сходимости) Если при любом
|
.
.
всех точек, в которых сходится ряд 
называется областью поточечной сходимости этого ряда.
такая, что для любой точки 
число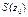 
является суммой числового ряда 
, называется суммой функционального ряда.
.
сходится в области D к функции 
, и 
− некоторое множество.
называется равномерно сходящимся
, если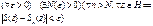
,
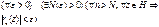
Если такой номер 
зависит не только от 
, но и от 
, т.е. 
,
.
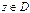выполняется неравенство 
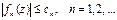, а числовой ряд 
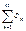сходится, то функциональный ряд 
сходится в области 
равномерно.
