Часть I
ТАКСАЦИЯ ОТДЕЛЬНЫХ ДЕРЕВЬЕВ ББК 43.90.я19 С59 УДК 630*53(075)
Рецензенты: Кафедра лесоводства Башкирского государственного аграрного университета (зав. кафедрой д-р с.-х. наук, проф., акад. Аоо А.Ф. Хайретдинов); д-р с.-х. наук, доц. кафедры лесоустройства и охраны леса Московского государственного университета леса В.В. Заварзин.
ТАКСАЦИЯ ЛЕСА Часть II ТАКСАЦИЯ НАСАЖДЕНИЙ Рецензенты: Кафедра радиационной экологии и жизнеобеспечения Брянской государственной инжерно-технологической академии (зав. кафедрой д-р с.-х. наук, профессор, заслуженный лесовод России, академик Е.С. Мурахтанов) Кафедра лесоводства Ижевской государственной сельскохозяйственной академии (канд. с.-х. наук, доцент Т.В. Климачева д-р. с.-х. наук, профессор, академик МАНЭБ, заслуженный лесовод России А.А. Корепанов канд. с.-х. наук, доцент В.М. Максимов и профессор В.С. Мурзин (Воронежская государственная лесотехническая академия
ТАКСАЦИЯ ЛЕСА Часть III УЧЕБНАЯ ПРАКТИКА Рецензент: д-р. с.-х. наук, профессор, заведующий кафедрой лесных культур А.К. Касимов Соколов П.А С 59 Таксация леса. 3 части. Таксация отдельных деревьев. Таксация насаждений. Учебная практика: учебно-методическое пособие.-Ижевск:ФГОУ ВПО Ижевская ГСХА, 2007.-213 с.
Компютерное оформление Поздеев Д.А.
СОДЕРЖАНИЕ
ТАКСАЦИЯ ЛЕСА Часть I ТАКСАЦИЯ ОТДЕЛЬНЫХ ДЕРЕВЬЕВ Введение Вернутся в содержание Лесная таксация (лат. taxatio – оценка) является важнейшей профилирующей и методологической дисциплиной, рассматривающей методы всестороннего учета лесных ресурсов. Основными объектами лесной таксации являются: • отдельные деревья и их части; • совокупность отдельных деревьев, произрастающих в разных древостоях, но объединенных по какому-либо признаку (например, по выходу спецсортиментов); • совокупность деревьев, произрастающих совместно (древостои элементов леса); • насаждение как совокупность отдельных древостоев — элементов леса и других ярусов растительности; • лесной массив как совокупность насаждений, занимающих значительные площади; • недревесные ресурсы леса, представляющие биологическое разнообразие растительного покрова лесных ценозов, включая фитомассу; • заготовленная древесина и недревесная продукция. Лесная таксация призвана заниматься разработкой методов количественного и качественного учета древесины и недревесной продукции как в статике, так и в динамике, т.е. с учетом изменений насаждений с возрастом, а также лесосырьевых ресурсов в целом. Биологический характер объектов лесной таксации обуславливает широкое применение методов вариационной статистики, математического моделирования, биометрии. С другой стороны, многообразие объектов и целей таксации требует разного подхода к методам и технике оценки лесных ресурсов. На основе массовых наблюдений разработаны основные способы глазомерно-измерительной и перечислительной (с предварительным перечетом деревьев) таксации. Как любая другая наука, лесная таксация должна рассматриваться во взаимосвязи с другими дисциплинами, а именно: математикой, экологией, физикой, химией, ботаникой, дендрологией, геодезией, лесоведением и лесоводством, лесным товароведением, фитопатологией, лесоустройством, аэро- и космической фотосъемкой. В основу предлагаемой работы легли изданные ранее и рекомендованные Министерством общего и профессионального образования Российской Федерации учебные пособия (1998,2000) для студентов высших учебных заведений по специальностям 260400 – «Лесное хозяйство» и 260100 – «Лесоинженерное дело».
1. ТАКСАЦИЯ СРУБЛЕННЫХ ДЕРЕВЬЕВ И ИХ ЧАСТЕЙ 1.1.1 Единицы измерения и инструменты Вернутся в содержание Отдельное дерево является основным объектом изучения в лесной таксации. По естественным признакам оно делится на части: ствол (50-90 % общего объема), крона (5-25 %), корни (5-30 %). По производственному назначению различают деловую древесину ствола (учитывается без коры), дровяную древесину и отходы. Деловая и дровяная древесина составляет ликвидную часть ствола, в отходы включается кора деловой части и вершинка (диаметром около 3 см у основания). Ликвидную часть можно также получить и из кроны дерева. Отходы — понятие условное, т.к. вся фитомасса дерева может служить сырьем для получения ценных продуктов (технологическая щепа, древесные плиты, арболит, биологически активные вещества, клеточный сок, аскорбиновая кислота, хлорофилл, эфирные масла, каротин, протеин, клетчатка и др.). Древесина по объему учитывается в плотных и складочных кубометрах. Плотный кубометр представляет собой куб, сплошь заполненный древесиной; складочный кубический метр включает кроме плотной древесины промежутки, заполненные воздухом. Для перевода складочных кубометров в плотные применяют переводные коэффициенты, которые зависят от древесной породы, длины и толщины поленьев (табл. П17). Другими элементами измерения дерева являются возраст, диаметр, высота (длина), масса. Возраст определяется по числу годичных слоев у шейки корня (в практике - на пне с учетом высоты пня) с точностью до одного года. Диаметр измеряется в сантиметрах и миллиметрах, высота и длина в метрах, дециметрах, сантиметрах. Масса ствола и кроны измеряется в тоннах, центнерах и килограммах. Она может учитываться в сыром, воздушно-сухом и абсолютно сухом состоянии (табл. П18-20). Для измерения диаметров применяются приборы, основанные на различных принципах работы (использование измерительной линейки с подвижной и неподвижной ножками, измерение диаметра при помощи двух касательных к дуге окружности ствола, замер длины окружности ствола, использование оптических законов физики, метод фотографии древесного ствола и т.д.). Диаметры отдельных деревьев измеряют с точностью до 0,1 см в двух взаимно перпендикулярных направлениях. Для измерения массы деревьев (при перечете) учет ведется по ступеням толщины: I см, 2 см и 4 см. При отсчетах диаметры 0,5 и более ступени округляются вверх до следующей ступени, менее 0,5 ступени в расчет не принимаются. Для облегчения отсчетов округленных ступеней первая ступень наносится на мерную линейку в половинном размере. Для измерения высоты деревьев применяются высотомеры, конструкции которых основаны: • на тригонометрическом принципе (Макарова, Блюме-Лейса, эклиметр, «Метра», «Суунто», BH-I и другие); • геометрическом принципе подобия треугольников (Вейзе, Фаустмана, Христена, оптический Анучина, мерная вилка и другие); • наземном измерении с летательных аппаратов. Для определения возраста растущих деревьев используется возрастной бурав, представляющий собой пустотелый цилиндр с рукояткой, на конце которого нарезана резьба в форме шурупа. Бурав ввинчивается в дерево по радиусу до сердцевины, столбик древесины из цилиндра извлекается с помощью тонкой пластинки с зазубринами, заранее вставленной в полость цилиндра. Возраст дерева определяется по числу годичных слоев на столбике (керне) древесины. Подобную конструкцию, но с цилиндром меньшего размера, имеет приростной бурав для определения текущего периодического прироста диаметра ствола. При таксации кроны дерева используются крономеры разной конструкции и палетки. Подробное знакомство и работа с таксационными приборами и инструментами будут проводиться во время учебной практики. Основными таксационными показателями ствола, на увеличение которых направлены лесохозяйственные мероприятия, являются объем (V) и прирост объема (ZV). Остальные показатели, характеризующие продольную и поперечную форму ствола, сбег, полнодревесность, приросты высоты, диаметра и площади сечения, являются вспомогательными.
1.1.2 Определение объема ствола Вернутся в содержание Различают физические и математические методы определения объема ствола. Физические методы основаны на 1) законе Архимеда (ксилометрический метод) и нa 2) взвешивании стволов и вычислении объема по массе и удельному весу древесины (весовой способ) по формуле:
V=
где
Удельный вес древесины величина переменная, зависящая от многих факторов, поэтому весовой способ не является точным. Прежде чем приступить математическим методам определения объема ствола, рассмотрим форму продольного его сечения. Под формой ствола понимают его образующую по продольному сечению. Чаще всего при определении объема используют стереометрические формулы, основанные на уравнении Ньютона:
y2=AXr, (1.2)
где у – радиус поперечного сечения ствола, А – коэффициент, определяющий размер кривой, r – показатель формы кривой, для цилиндра r = 0 параболоида r = 1 конуса r = 2 нейлоида r = 3, Х – расстояние от основания до вершины. Разные части древесного ствола приравниваются к телам, образованным вращением различных кривых, при этом получается: в нижней части ствола – нейлоид, в средней – цилиндр, в верхней – параболоид второго порядка, вершинка – конус. На основании уравнения Ньютона выведены простые формулы определения объема ствола:
1) по срединному сечению (формула Губера):
V=g2
где g2 – площадь сечения на половине длины хлыста (часть ствола без вершинки) Vв – объем вершинки, определяемый по формуле конуса;
2) по среднему из двух сечений (формула Смалиана):
V=
где g0 – площадь сечения у основания ствола, gв – площадь основания вершинки;
3) по среднему из трех сечений (формула Ньютона-Рикке):
V=
Из-за больших корневых наплывов погрешности в определении объема ствола по формуле Смалиана могут достигать 65 %. Поэтому в практике применяют вариант этой формулы:
V=
где g0,2 и g0,8 – площади сечения соответственно на 0,2 и 0,8 высоты ствола, Для повышения точности в определении объема ствола применяют сложную формулу, когда ствол разделяют на отрезки равной длины (0,5; 1,0 и 2,0 м) и объем каждого отрезка определяют по формуле срединного сечения. При этом число отрезков должно быть не менее 8-12. Рекомендуется при длине ствола 15 м и более брать 2-метровые, 8-14 м – 1-метровые, 5-7 м и менее – 0,5-метровые отрезки. Формула в этом случае будет иметь вид:
V=V1+V2+V3+…+Vn+Vв=g1
где V1,V2… – объемы отрезков, g1, g2… – площади срединных сечений отрезков,
Объем каждого отрезка можно определить также по формуле Смалиана или Ньютона-Рикке. При вычислении площадей сечений стволов, а также объемов однометровых цилиндров можно использовать табл. П1. По этой же таблице определяется диаметр, если известна площадь сечения. Простые и сложные формулы используются и для вычисления объема отдельных сортиментов. Пример исходных данных и определение таксационных показателей ствола срубленного дерева приводится в табл. 1.1. Объем ствола в коре, вычисленный по сложной формуле срединного сечения, составит:
V=V1+V3+V5+…+Vn+Vв=g1 +g25)
В формуле g1,g3…,g25 – площади сечений в м2 в коре на середине 2-метровых отрубков, т.е. на нечетных метрах, g26 – площадь основания вершинки, длина которой составит:
Объем первого от комля сортимента длиной 6,5 м составит:
V6,5=g1
где g1, g3… – площади сечений без коры на нечетных метрах. Подобный расчет делается для вычисления объема следующего сортимента, при этом оставшиеся 1,5 м четвертой двухметровки относятся к этому сортименту и т.д. Объем сортиментов, т.е. отрезков ствола, предназначенных для тех или иных целей, можно вычислить также по таблицам объемов бревен – ГОСТ 2708-75 «Лесоматериалы круглые. Таблицы объемов» (табл. П2), а также по таблицам объемов цилиндров, приравнивания объем сортимента к объему цилиндра, основанием которого является площадь срединного сечения бревна. В нашем примере верхний диаметр без коры 6,5-метрового сортимента, найденный путем интерполяции, равен 21,4 см. По ГОСТ 2708-75 при округленном диаметре 22 см объем равен 0,31 м3. По таблицам же объемов цилиндров объем будет равен:
V6,5 =
где g3,2 – площадь сечения на середине длины сортимента (3,2 м),
Таблица 1.1 – Порода сосна, возраст 128 лет, высота 27,3 м
1.1.3 Сбег и видовые числа Вернутся в содержание Сбегом ствола называется уменьшение его диаметров по направлению от нижнего торца к вершине. Различают два вида сбега: действительный и средний, как тот, так и другой могут быть абсолютным (в см) и относительным (в долях или процентах от диаметра, например, от диаметра на высоте 1,3 м). Действительный сбег представляет собой изменение диаметра ствола на протяжении 1 м, т.е. на каждый конкретный метр длины ствола в см. Он может выражаться значениями самих диаметров, обмеренных через каждый метр ствола (в практике для удобства диаметры показывают через каждые 2 м), что дает возможность вычертить образующую ствола и точно воспроизвести его форму, или через разность двух смежных диаметров, отстоящих друг от друга на 1 м. Действительный сбег характеризует быстроту уменьшения диаметров в разных частях ствола, но не дает представления о форме последнего. Средний (или конический) сбег представляет изменение диаметра в среднем на 1 м длины данного отрезка: бревна, хлыста или ствола в целом. Абсолютный средний сбег любого усеченного отрезка ствола находят путем вычитания верхнего диаметра из нижнего и делением общего сбега в см на число метров длины отрезка. Относительный средний сбег – это отношение диаметров в любой точке ствола к диаметру на 1,3 м или 0,1 высоты ствола. Различают еще комлевой сбег как разность между диаметрами ствола на пне и 1,3 м. По величине среднего сбега можно дать характеристику ствола (табл.1.2).
Таблица 1.2 – Характеристика среднего сбега ствола
Коэффициент формы ствола является одним из показателей относительного сбега соответствующей части ствола, он вычисляется путем деления диаметра, измеренного на данной высоте, на диаметр на высоте 1,3м. В практике различают четыре коэффициента формы ствола в зависимости от того, в какой точке ствола будет взят диаметр для вычисления:
q0=
q1=
q2=
q3= где d0, d1, d2, d3 – диаметры ствола, взятые на шейке корня, 1/4, 1/2 и 3/4 высоты ствола; d1,3 – диаметры на высоте 1,3 м.
Наиболее важным является второй коэффициент формы ствола – входной признак в различные таблицы. Форму ствола данный коэффициент не характеризует, так как при одной и той же форме ствола он тем меньше, чем больше высота. Например, у параболоида q2 равен: 0,82 при h = 5 м; 0,76 при h = 10 м; 0,73 при h = 20-25 м; 0,72 при h =30-40 м. При изменении q2 на 0,01 объем ствола изменяется на 1,6-1,5 %. Применительно к примеру, указанному в табл. 1.1, коэффициенты формы в коре составят:
q0=
q2=
Показателями формы ствола являются «классы формы» (по проф. Н.В.Третьякову), получаемые путем деления разных диаметров ствола на диаметр, взятый на четверти высоты. Так, второй класс формы в нашем примере будет равен:
q2/1=
По значениям коэффициента и класса формы можно дать характеристику сбежистости ствола.
Таблица 1.3 – Характеристика сбежистости ствола
Коэффициентом полнодревесности ствола является видовое число, т.е. отношение объема ствола к объему одномерного цилиндра, имеющего с деревом одинаковую высоту и основание, равное площади сечения ствола на определенной высоте в нижней его части. Различают старое видовое число, когда площадь основания цилиндра берется на 1,3 м, нормальное – на 0,1 высоты ствола и другие. В практике наиболее распространено старое видовое число:
где g1,3 – площадь сечения ствола на 1,3 м,
Видовое число показывает, какую часть объема одномерного цилиндра занимает объем ствола и служит в качестве переходного коэффициента от легко устанавливаемого (по g1,3 и h) объема цилиндра к объему ствола. Существует связь между коэффициентом формы и видовым числом:
по Вейзе:
формула справедлива лишь для параболоида;
по Кунце
где с – поправочный коэффициент, зависящий от q2 и h;
по Шифелю
Профессор М.Е. Ткаченко вывел закон формы стволов: при равных высотах, коэффициентах формы q2 и диаметрах на 1,3м стволы всех пород имеют близко равные видовые числа. Им составлена таблица всеобщих видовых чисел в зависимости от высоты и второго коэффициента формы (табл. П14).
1.1.4 Прирост отдельных деревьев Вернутся в содержание В процессе жизнедеятельности деревьев на стволах, ветвях и корнях происходит ежегодное наращивание слоев древесины, что ведет к увеличению их размеров. Увеличение размерных показателей дерева (диаметр, высота, площадь сечения, объем) с возрастом называется приростом, он бывает всегда положительной величиной и обозначается буквой Z. У относительных показателей стволов (q2 и Различают текущий и средний прирост. Текущий прирост – это увеличение таксационного показателя за определенный период времени. По величине учетного периода различают: • текущий годичный прирост – увеличение таксационного показателя за один определенный, чаще всего за последний год жизни дерева; • текущий периодический – увеличение за целый, сравнительно короткий период, обычно за 3; 5 или 10 лет; • полный текущий прирост – это значение размерного показателя в момент наблюдения. Средний прирост—это увеличение таксационного показателя в среднем за один год какого-либо периода времени. В зависимости от периода наблюдения различают: • средний периодический прирост, т.е. увеличение показателя в среднем за один год периода (3; 5; 10 лет) жизни дерева; • общий средний прирост – увеличение показателя в среднем за один год всей жизни дерева. Прирост таксационных показателей измеряется в абсолютных величинах в тех же единицах, что и сами таксационные показатели. Текущий годичный прирост диаметра (Zdтек. год) в силу малой его величины практически в лесной таксации не используется, чаще он применяется в дендрохронометрии. Взамен текущего годичного пользуются средним периодическим приростом диаметра. Текущий периодический прирост диаметра (Zdтек. пер.) в любой точке срубленного дерева определяется путем вырубания щепы с отвесной стенкой, содержащей t годичных слоев (3; 5; 10). Измеренная с точностью до мм величина прироста радиуса удваивается (при более точных расчетах прирост измеряют по двум взаимно перпендикулярным радиусам). Важное значение в разработке методов определения прироста запаса леса имеет линейный прирост, т.е. изменение текущего периодического прироста диаметра подлине ствола. Различают следующие его виды: • возрастающий; • падающий: • постоянный; • вогнутый; • выпуклый. Основная форма линейного прироста в молодняках – возрастающий прирост, с возрастом он переходит в постоянный, в стадии старения – вогнутый и выпуклый. При осветлении дерева появляется падающая форма прироста. В разновозрастных древостоях основной формой является постоянный прирост. Текущий периодический прирост площади сечения (Zgтек. пер.) представляет собой разность между конечным gа и начальным gа-1 ее значением:
Zgтек. пер.=ga – ga-t (1.18) Для вычисления требуется измерить конечный (в момент наблюдения) диаметр без коры dа, его прирост Zdтек. пер и вычислить бывший (начальный) диаметр da-t:
da-t=da – Zdтек. пер. (1.19)
По полученным диаметрам определяют соответствующие площади сечения и подставляют в формулу (1.18). Текущий периодический прирост высоты (Zhтек. пер.) – это сумма длин годичных побегов, образовавшихся за t лет. Определяется подсчетом числа вершинных мутовок, по следам кольцевых рубцов или последовательным перерубанием вершины ствола (у основания вершины, приросшей за последние t лет, должно быть t годичных слоев). Текущий периодический прирост объема ствола определяют как разность двух объемов – конечного и начального:
ZVтек. пер.=Va – Va-t (1.20)
Отсюда следует, что для его определения возможно использовать все методы определения объемов стволов, которые рассмотрены выше. По степени точности все способы определения ZVтек. пер можно подразделить: • на сложные, когда объем ствола вычисляется по коротким отрезкам; • упрощенные – объем вычисляется по удлиненным отрезкам; • приближенные – способы построены на разных допущениях. Для определения величины текущего прироста объема по сложным формулам у лежащего ствола на середине отрезков измеряют диаметры в коре, двойную толщину коры, текущий прирост диаметров, у дерева в целом – текущий прирост высоты Zhтек. пер. . По этим данным определяют диаметры без коры da и диаметры, бывшие t лет назад da-t. Высота, бывшая t лет назад, определяется по формуле:
ha-t=ha – Zhтек. пер.. (1.21)
Далее определяют объемы стволов без коры (Va и Va-t) по сложной формуле срединного сечения. При упрощенных методах бывшую высоту ствола разбивают на небольшое число отрезков (3-5), равных по длине. Объемы их определяют по одной из простых математических формул (чаще по срединному сечению). По исследованиям проф. МЛ. Дворецкого (1964), точность определения текущего прироста объема ствола находится в прямой зависимости от количества отрезков, на которые разбит ствол. Рекомендуется при точных расчетах ствол разбивать не менее чем на 10 отрезков. Приближенные способы определения ZVтек. пер основаны на тех или иных допущениях: а) способ по срединному сечению:
ZVтек. пер=(g2–γ2)
где g2 – площадь сечения ствола в возрасте а на середине бывшей высоты; γ2 – площадь сечения ствола в возрасте a-t лет на середине бывшей высоты. При этом предполагается, что ширина годичного кольца на половине бывшей высоты является средней для всего ствола. Способ показывает сред
|

 , (1.1)
, (1.1) – масса ствола в т,
– масса ствола в т, – удельный вес древесины в т/м3.
– удельный вес древесины в т/м3.
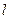 х+Vв, (1.3)
х+Vв, (1.3) , (1.4)
, (1.4)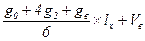 . (1.5)
. (1.5) , (1.6)
, (1.6) =(g1+g2+g3…+gn)
=(g1+g2+g3…+gn)  =2(g1+g3+g5…
=2(g1+g3+g5…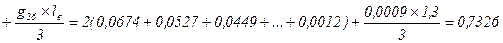 м3. (1.7)
м3. (1.7) м3, (1,8)
м3, (1,8) м3, (1.9)
м3, (1.9) ; (1.10)
; (1.10) ; (1.11)
; (1.11) ; (1.12)
; (1.12) ; (1.13)
; (1.13) q1=
q1= 
 q3=
q3= 
 = 0,80. (1.14)
= 0,80. (1.14)
 , (1.15)
, (1.15) – высота ствола.
– высота ствола. , (1.16)
, (1.16) , (1.17)
, (1.17)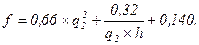
 ) с возрастом происходит изменение их значений, они могут быть как отрицательными, так и положительными величинами, обозначаются буквой Δ
) с возрастом происходит изменение их значений, они могут быть как отрицательными, так и положительными величинами, обозначаются буквой Δ 


