Единицы измерения и учета толщины, длины срубленных и растущих деревьев, объема деревьев и запаса насаждений. Погрешности измерений.
Единицы измерения. Толщина дерева, диам. бревна, длина, высота растущих деревьев, площадь поперечных сечений стволов, объем лесной продукции (реже опр-ют массу лесной продукции). При опрн-нии этих параметров основываются на мере длины, поверхности, объема, веса. Все виды измерений имеют свои учетные единицы. Эталоном меры длины является метр. 1м = 10дм = 100см = 1000мм. Площади в м2: 1 м2 = 100дм2 = 10.000см2. (кв.м). Запас или объем (куб.м): 1м3 = 1000дм3 = 1000.000см3; 1га = 10ар, 100га = 1км2. тыс.м3, млн м3, млрд м3 – это метрическая система мер. В целях упрощения измерений и последующего нахождения объема, величины d округляются до ближайших четных размеров (отличается на 2-4см) ступени толщины бывают двухсантиметравые и 4см. В России на h 1,3 (в США на h=1,38, в Японии h =1,25). Высоту измеряют в м и см, диаметр в см. Площадь сечения дм2, м2, см2. Площадь при переводе на 1га = 10.000м2, 1тыс.км2 = 10тыс.га Проекции крон измеряются в переводе на 1га 1тыс.км2 = 10тыс.га 1млн км2 = 100млн га. Кол-во древесины (объем), для насаждений – запас. Кубатура пиломатериала (объем дерева), в древостое – запас, на пробе, на лесосеке, в лесном квартале, лесничестве, лесхозе. Насаждение – определенный участок древесно-кустарниковой растительности одной породы, производительности, возраста, густоты. Включает: древостой, подрост, подлесок. Основная единица V и запаса м3: плотный м3 (пл.м) и складочный м3 (скл.м). Досковый фут в США на 30-48 см, толщиной 24см единица учет лесной продукции. В футах нельзя посчитать объем бревна, а только объем досок. Корд 4х4х8 (фунт), пен = 1/5 кордов. Измерения – действие, устанавливающее численной отношение м/д измеряемой величиной и заранее выбранной единицей измерения, не редко именуемой масштабом или эталоном, древнейшее измерение. В системе измерения Весы – вес, часы – время и т.д. В современном производстве большую роль играют высокоточные измерения. Менделеев: «наука начинается с тех пор, как начинают измерять». Измерения делятся на: - прямые результат известен непосредственно после измерения. - косвенные результаты получают на основание простых измерений, нужно иметь измерения нескольких величин. Это можно представить формулой: y = F (x1 + x2 +…x3) - совокупные измерения, их результат получают из совокупности прямых измерений и ряда вычислений, которые выполняются по соответствующим формулам ПР: составление прогноза погоды. В развитии тех-кого прогресса огромное значение имеют автоматическое измерение, без участия человека (термометр, часы). При таксации леса осуществляющей массовые измерения автоматические приборы и инструменты до сих пор не применяются. О погрешностях. Всякое измерение неизбежно связано с погрешностями обусловленными целым рядом факторов. Для получения результатов измерения близкого к действительному разработаны методики, выявляющие возможные источники погрешностей. Если величина и знак погрешности известны, то приближенные к действительному значению измеряемой величины осуществляется путем сложения поправки с полученной величиной. Погрешности могут быть со знаком + и -. Математическая статистика различает: случайные и систематическиепогрешности. При измерении h, d дерева могут быть не точности самого инструмента – это систематические ошибки. ПР: для промера кварталов может использоваться стальная лента, троса (50м). При каждом измерении систематическая ошибка накапливается, увеличивается пропорционально числу измерений (суммируется). Промеры не должны превышать допуски для этого вида. Свойства случайных ошибок: 1. Малые ошибки встречаются чаще, чем большие. 2. При множестве измерений ошибки с + и – равновероятны. 3. Случайные ошибки распределяются в соответствии с законом распределения вероятности, графически изображается кривой Гаусса-Лапласа. График (кривая нормального распределения ошибок): N / ± 68,27%. N- кол-во измерений, - ошибки. Все измерения с ошибками: = ±95,45%; 3 = ±99,7% Для опр-ния точности среднеарифметической величины используют методы математической статистики. С этой целью строятся вариационные ряды и их статистические показатели, т.е. выявляются средние значения ошибки. Среднеквадратическое отклонение вычисляется:
Ошибка среднего значения
Коэф-т изменчивости (варьирования): С (ω) = ± 11,2% Точность Задача: чтобы точность была 2%.
|


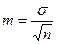 ; ПР: m = ± 0,43
; ПР: m = ± 0,43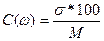 ;
;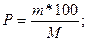 Р = 3,58%.
Р = 3,58%. 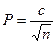 ;
;