Методический подход к расчету распределения плотности поглощаемого элементами КА потока излучения.
При радиационном теплообмене между реальными нечерными поверхностями излучение, испускаемое некоторой поверхностью попадает на другие поверхности в результате многократного отражения с частичным поглощением излучения при каждом его взаимодействии с поверхностями. При таком процессе трудно уследить за прохождением излучения и за всеми актами поглощения. Но это и не нужно делать, если воспользоваться известным обладающим широкими возможностями методом, называемым или методом лучистого сальдо, или зональным методом. Применяя этот метод и используя принятые обозначения, запишем для стационарного режима уравнение теплового баланса для каждого из
где Использую соотношения (4.5), исключим из уравнений (4.4) члены, содержащие После простых преобразований система примет следующий вид:
где
При известных правых частях уравнений (4.6) можно определить неизвестные величины Определив в результате решения системы уравнений (4.6) плотности исходящих от каждой грани эффективных тепловых потоков, можно вычислить с помощью соотношений (4.7) распределение температур
Однако в формировании поля температур нижней и верхней бленд телескопа, его тубуса и, особенно, в формировании поля температур зеркал существенную роль может играть теплопроводность материалов отмеченных элементов. Поэтому возникает необходимость решения задач теплопроводности для каждого фрагмента КА, для которого теплопроводность может играть заметную роль в формировании поля температур. Результаты расчета распределения плотности эффективных тепловых потоков по поверхности элементов КА служат всего лишь основой для определения граничных условий решения задач теплопроводности для этих частей КА. Причем граничными условиями служат не сами величины плотности эффективных тепловых потоков, а величины локальной плотности поглощаемых элементами поверхности потоков излучения (
|

 элементов рассматриваемой системы:
элементов рассматриваемой системы: = 0 (4.4),
= 0 (4.4), (4.5)
(4.5) , и получим систему
, и получим систему 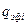 уравнений, правые части которых будут зависеть от величины и распределения по поверхности КА подводимой извне или изнутри тепловой энергии.
уравнений, правые части которых будут зависеть от величины и распределения по поверхности КА подводимой извне или изнутри тепловой энергии.
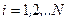 (4.6)
(4.6)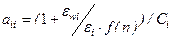 ,
, 
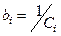 ,
, 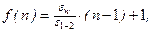
 ,
,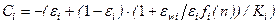
 ,
,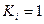 -для односторонних поверхностей,
-для односторонних поверхностей, 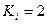 - для двусторонних поверхностей.
- для двусторонних поверхностей. , методика вычисления которых излагалась в предыдущем разделе.
, методика вычисления которых излагалась в предыдущем разделе.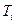
 по граням исследуемого объкта, но температур, которые имели бы место в телескопе при отсутствии теплопереноса за счет теплопроводности материала его конструктивных и оптических элементов. Это выражение имеет вид:
по граням исследуемого объкта, но температур, которые имели бы место в телескопе при отсутствии теплопереноса за счет теплопроводности материала его конструктивных и оптических элементов. Это выражение имеет вид:
 ). Плотность поглощаемого
). Плотность поглощаемого  гранью теплового потока определяется следующим очевидным соотношением:
гранью теплового потока определяется следующим очевидным соотношением: 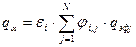 . Для решения задачи теплопроводности необходимо задать непрерывную функцию, характеризующую распределение плотности поглощаемого рассматриваемой поверхностью потока излучения. Поэтому решению задач теплопроводности должно предшествовать решение задач аппроксимации дискретно заданных функций распределения
. Для решения задачи теплопроводности необходимо задать непрерывную функцию, характеризующую распределение плотности поглощаемого рассматриваемой поверхностью потока излучения. Поэтому решению задач теплопроводности должно предшествовать решение задач аппроксимации дискретно заданных функций распределения  непрерывной функцией. Аппроксимацию целесообразно осуществлять с помощью сплайн-функции, где в качестве базовых функций лучше всего использовать кубические полиномы.
непрерывной функцией. Аппроксимацию целесообразно осуществлять с помощью сплайн-функции, где в качестве базовых функций лучше всего использовать кубические полиномы.


