Общая характеристика математических моделей,применяемых на различных этапах проектирования КА.
Быстрое развитие космической техники, сопровождающееся качественным отличием каждой новой серии аппаратов от предыдущей, диктует необходимость использования новых принципов и технических решений при создании СОТР. Причем, принципов и решений, ранее не апробированных в космическом полете и в условиях наземных экспериментов. Поэтому уже на стадии разработки технических предложений возникает необходимость в оценке эффективности предлагаемых к использованию средств обеспечения теплового режима, что делается с помощью достаточно убедительных математических моделей. Можно отметить следующие основные задачи, решаемые с помощью математических моделей на различных стадиях разработки, создания и эксплуатации КА: - выяснение возможности построения СОТР при использовании определенных средств регулирования внешнего и внутреннего теплообмена; - определение параметров этих средств и проведение тепловых расчетов для сравнения различных вариантов и выбора наиболее оптимального из них; - определение необходимой площади радиационных поверхностей; -выбор радиационно-оптических характеристик для внешних поверхностей; -выбор требований к теплоизоляции элементов конструкции от окружающего пространства; -оценка поля температур по корпусам и элементам конструкции при выбранных средствах обеспечения теплового режима; - определение расхода теплоносителей, мест установки элементов, регулирующих теплообмен, параметров теплообменных устройств и т. д.; - определение параметров систем с расходом рабочих тел, если такие системы используются в числе других средств обеспечения теплового режима КА; -выработка требований к конструкции с учетом требований СОТР. Математическое моделирование теплового состояния КА дает возможность наиболее полно и однозначно представить и количественно оценить тепловые взаимодействия между элементами КА, выделить основные параметры, характеризующие эти взаимодействия, проверить влияние этих параметров на температуры тех или иных элементов и, в конечном счете, получить зависимости, позволяющие прогнозировать возможные температуры при любых внешних и внутренних тепловых возмущениях. Первым и непременным этапом любого теплового расчета является составление тепловой схемы. Тепловая схема представляет собой схематическое изображение рассматриваемых узлов КА, включая элементы СОТР (в случае анализа теплового режима КА в целом) или такое же изображение какого-либо элемента КА при решении частной задачи, с указанием всех существенных тепловых связей, а также внешних и внутренних тепловых воздействий. При составлении тепловой схемы выделяются узловые точки, характеризующие температуру, формируются допущения в части возможного упрощения изображаемых процессов. В итоге тепловая схема является наглядным представлением тех взаимодействий, которые предполагается анализировать при дальнейших расчетах. Уже на этой стадии представляется возможным, сформулировав граничные условия и возможные диапазоны характеризующих их величин, ограничить линии тепловых взаимодействий некоторыми наперед заданными тепловыми состояниями сопряженных элементов. На основе составленной тепловой схемы для дальнейшего перехода к математической модели создается расчетная схема - схемное или словесное описание тепловых взаимодействий элементов, выделенных в тепловой схеме, и допущений, принятых с целью математического анализа процессов теплообмена. Весьма распространенным способом построения математической модели теплообмена КА является метод конечных элементов (метод узлов), при использовании которого исследуемый объект разбивается на части (узлы) с однородным температурным полем. Тепловое взаимодействие узлов между собой и окружающим пространством описывается уравнениями элементарного теплового баланса, которые составляются на основе тепловой схемы, представляющей собой схематичное изображение выделенных узлов КА, включая элементы системы обеспечения теплового режима, с указанием всех существенных тепловых связей, а также внешних и внутренних тепловых воздействий. Тепловая схема дает наглядное представление о тех взаимодействиях, которые будут описываться аналитически. Уравнения теплового баланса узлов можно записывать по-разному, например в следующем виде:
где Во многих работах, например в [1,7,14], член уравнения теплового баланса, характеризующий результирующий к поверхности На разных стадиях разработки и создания КА, возникают разные требующие теплового расчета задачи, поэтому появляется потребность в различных по сложности математических моделях. Например, на стадии проектирования КА, когда конструкция его окончательно не определена и основной задачей теплового расчета является выбор средств СОТР и определение их параметров, применяют упрощенные модели с минимальным количеством элементов и тепловых связей между ними. В пределе могут быть модели теплового режима аппарата, состоящие из одного элемента. Например, рассматривают аппарат как однородное тело, имеющее определенные геометрические размеры, массу, теплофизические свойства. Как отмечается в [7], такая модель позволяет оценить возможность и достаточность пассивных средств обеспечения теплового режима для рассматриваемого аппарата. Иногда аппарат делят на элементы по их функциональному признаку, например, выделяют оболочку, газ, циркулирующий в отсеке, группу однородных по тепловыделению приборов и т.п. При этом предполагается, что тепловое состояние каждого элемента модели достаточно достоверно может быть охарактеризовано некоторой средней температурой, относительно которой может быть записан его тепловой баланс. Простые модели, учитывающие только главные тепловые связи, позволяют быстро оценить большое количество вариантов СОТР и выбрать наиболее оптимальную. Однако любой расчет по упрощенной модели может иметь смысл только тогда, когда известны пределы возможных отклонений локальных температур в элементе от используемого в приближенном расчете среднего их значения. Поэтому составлению упрощенной модели предшествует большая работа, связанная с оценкой возможных полей температур в элементах конструкции, c расчетной проверкой справедливости упрощающих допущений, основанных на прошлом опыте поэлементного анализа теплового режима КА и на результатах решения частных задач теплообмена. Здесь важное значение имеет интуиция исследователя, его опыт. Упрощение математической модели может быть достигнуто за счет представления ее в виде совокупности отдельных сравнительно небольших моделей, сопряженных между собой граничными условиями. Каждая из этих моделей описывает теплообмен определенной части КА, что позволяет вести тепловые расчеты отдельных частей аппарата независимо друг от друга. По мере конкретизации конструкции КА и средств обеспечения теплового режима возникает потребность в более сложных математических моделях. Так на стадии разработки рабочей документации для проверки правильности принятых технических решений проводятся поверочные расчеты с использованием математических моделей, насчитывающих десятки и даже сотни узлов. Расчеты на основе таких моделей являются трудоемкими, но не сколько из-за большого объема вычислений (современные компьютеры легко справляются с этой задачей), сколько из-за необходимости подготовки и ввода большого количества исходных данных – коэффициентов в уравнения системы, характеризующей тепловое состояние узлов КА. Поэтому модели с большим количеством узлов могут быть эффективны в расчетах на той стадии, когда конструкция уже разработана и проведен цикл экспериментальных исследований по определению различных теплофизических характеристик элементов КА и оценке тепловых связей между ними. Появление КА, имеющих в своем составе крупногабаритную аппаратуру для проведения астрофизических исследований за пределами земной атмосферы привнесло большие трудности в процесс теплового проектирования таких космических объектов, особенно космических телескопов. Трудности обусловлены, во-первых, сложностями организации упорядоченного теплообмена в негерметичных отсеках с весьма протяженными элементами непростой геометрической формы при существенных ограничениях на уровень потребляемой ботовой электроэнергии, а во-вторых, исключительно жесткими требованиями к однородности поля температур по некоторым оптическим элементам, имеющим существенные геометрические размеры. Обсуждаемые выше математические модели, основанные на использовании метода узлов, не могут претендовать на роль надежного инструмента исследования теплового режима уже разработанных телескопов и для поиска новых более эффективных способов обеспечения теплового режима вновь создаваемых телескопов, поскольку при большом количестве элементов, на которые разбивается исследуемый объект, эти модели сложны в эксплуатации из-за исключительно большого объема работы по подготовке исходной информации об исследуемом объекте. Поэтому для исследования теплового состояния таких объектов как космические телескопы нужны другие математические модели, которые, обеспечивая высокую точность расчета полей температур на протяженных и сложных по геометрической форме поверхностях, в то же время, были бы предельно простыми в отношении ввода исходной информации об исследуемом объекте. Рассмотрим одну из таких моделей, апробированную в процессе теплового проектирования ультрафиолетового и рентгеновского телескопов. При этом следует заметить, что рассматриваемую ниже модель можно использовать для исследования теплового состояния любого негерметичного КА. Математическую модель можно рассматривать как совокупность трех отличающихся по функциональному назначению частей, которые могут реализовываться в виде компьютерных программ независимо друг от друга. Исходной информацией для первой части математической модели является геометрическая модель исследуемого объекта. Эта информация вводится в виде координат точек поверхностей объекта, которые окажутся вершинами треугольных граней поверхностей многогранников, аппроксимирующих, по сути дела реальные фрагменты поверхности КА. Координаты точек вводятся в любой связанной с объектом системе координат, например, в цилиндрической. На основании этой информации определяются численные значения угловых коэффициентов между всеми элементами рассматриваемой части КА, поверхности которых способны поглощать падающее на них излучение и испускать энергию собственного теплового и отраженного излучения. Элементы, на которые разбиваются все радиационные поверхности представляют собой треугольные грани с характерными размерами, обеспечивающими достаточную однородность температурного поля в пределах каждой грани. Расчет угловых коэффициентов осуществляется с учетом возможного взаимного затенения одних элементов другими. В рамках второй модели осуществляется расчет поля температур в КА, формируемом за счет внутреннего и внешнего лучистого теплообмена, а также за счет подводимой к некоторым частям КА тепловой энергии от бортовых источников электропитания. Исходной информацией для данной программы являются радиационные характеристики поверхностей элементов КА, а также величины и распределение подводимых мощностей. В этой же части модели осуществляется проверка точности расчета поля температур путем сопоставления энергии, подводимой к КА извне и от внутренних источников тепловыделений, с энергией рассеиваемой КА за счет излучения при наличии того температурного поля, которое определено в результате реализации первой и второй частей модели. Первые две части модели дают возможность определить температуры в конечном числе точек без учета теплопроводности материала элементов КА. Однако возникает необходимость в получении более точной информации о температурном поле в некоторых частях КА. Для этого в третьей части модели осуществляется аппроксимация дискретных значений плотности эффективных тепловых потоков, исходящих от каждой грани многогранных поверхностей, аппроксимирующих поверхности КА, непрерывными значениями, что дает возможность далее в рамках третьей части модели решать задачи двумерной и одномерной теплопроводности с целью более точного определения характера распределения температур отдельных частей КА.
|

 ,
,  ,
,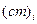 - теплоемкость
- теплоемкость  -го узла;
-го узла;  площадь поверхности
площадь поверхности  - величина средней плотности поглощаемого поверхностью
- величина средней плотности поглощаемого поверхностью  - коэффициент, характеризующий термическую проводимость тепловых связей между
- коэффициент, характеризующий термическую проводимость тепловых связей между  ым и
ым и 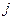 - ым элементами (это может быть произведением коэффициента теплоотдачи от газа или жидкости к стенке на площадь омываемой поверхности, это может быть величина, обратная контактному термическому сопротивлению и т.п.);
- ым элементами (это может быть произведением коэффициента теплоотдачи от газа или жидкости к стенке на площадь омываемой поверхности, это может быть величина, обратная контактному термическому сопротивлению и т.п.);  - коэффициент, зависящий от степени черноты, площади поверхности и ориентации как самого
- коэффициент, зависящий от степени черноты, площади поверхности и ориентации как самого  - величина внутренних тепловыделений в
- величина внутренних тепловыделений в 
 ), то сумма записывается в виде -
), то сумма записывается в виде -  .
.
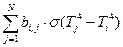 . Такой вид записи представляется не совсем корректным, т.к. это выражение является по существу результатом изолированного рассмотрения теплообмена между каждой парой элементов
. Такой вид записи представляется не совсем корректным, т.к. это выражение является по существу результатом изолированного рассмотрения теплообмена между каждой парой элементов 


