Координация
Выполнить рабочие чертежи деталей ________ и аксонометрию детали _________ на формате А2
С 15 мая 2012 года корпорация Autodesk открывает для учебных заведений и стран СНГ новый образовательный портал - Autodesk Academic Resource Centre (http://www.autodesk.com/academic). Портал обеспечивает возможность БЕСПЛАТНОЙ загрузки образовательных лицензий полнофункциональных версий программных продуктов Autodesk для использования их в учебном процессе. * - Лицензии для личного домашнего использования студентами и преподавателями можно получить на сайте http://students.autodesk.ru
Задание 1. Выполнить эскизы деталей 1,2,3,4,8. Материал дет. поз. 1-4 – Сталь 25 ГОСТ 1050-88, дет. поз. 8 – Сталь 45 ГОСТ 1050-88. Задание 2. Выполнить технический рисунок дет. поз. 4. Эскизы и технический рисунок вместе с исходными данными подшить в альбом с титульным листом. Задание 3. Выполнить рабочие чертежи деталей ________ и аксонометрию детали _________ на формате А2
С 15 мая 2012 года корпорация Autodesk открывает для учебных заведений и стран СНГ новый образовательный портал - Autodesk Academic Resource Centre (http://www.autodesk.com/academic). Портал обеспечивает возможность БЕСПЛАТНОЙ загрузки образовательных лицензий полнофункциональных версий программных продуктов Autodesk для использования их в учебном процессе. * - Лицензии для личного домашнего использования студентами и преподавателями можно получить на сайте http://students.autodesk.ru
Семинар -2
Функции институтов
Координация
Проблема координации и способ ее институционального разрешения иллюстрируется на примере игры «правила дорожного движения», где существует два варианта возможного выбора: двигаться по левой или по правой стороне (по ходу движения). Требуется оставить только один, в противном случае неизбежны столкновения:
Табл. 1. Игра «правила дорожного движения»
Для того чтобы такой выбор оказался возможным без предварительного общения, необходимо, чтобы у игроков в головах имелось общее представление о том, как себя вести в такой неопределенной ситуации. Это общее представление может обеспечить институт, который содержит информацию о доступном наборе альтернатив в соответствующей ситуации выбора. В итоге у участников координационной игры исчезает необходимость каждый раз решать вопрос о том, как себя вести, чтобы избежать столкновения. Если координация осуществляется в результате взаимодействия агентов между собой, т.е. носит внутренний характер, тогда говорят о соглашении как механизме достижения кооперации. Если же координация происходит под воздействием внешнего влияния, тогда речь идет о принудительной форме координации. Таким образом, формально, координация – это выбор одного равновесия из многих эквивалентных.
Кооперация (задачу на дуополию не разбирайте, почитайте только выводы – в окрестности матрицы игры)
Институциональное решение проблем кооперации состоит в необходимости объединения интересов игроков с целью достижения наиболее эффективных результатов. Такого рода объединение интересов предполагает достижение коллективного согласия в группе игроков по поводу предполагаемых действий и именуется проблемой коллективных действий. Для того чтобы понять смысл кооперативной функции институтов, рассмотрим взаимодействие двух одинаковых фирм в рамках многопериодной (динамической) дуополии. Пусть есть две одинаковые фирмы, образующие дуополию. Допустим, что обратная кривая спроса на продукцию дуополии линейна:
причем
и получает прибыль
Можно показать, однако, что равновесие Курно-Нэша не является Парето-эффективным. Парето-эффективным будет другое состояние, реализующееся в случае, когда фирмы принимают решения совместно (и выступают на рынке как монополия). В этом случае оптимальный выпуск каждой фирмы оказывается равным
а прибыль каждой фирмы - больше прибыли Курно:
Таким образом, если фирмы будут принимать свои решения совместно, тогда они смогут получить наибольшую суммарную прибыль, достижимую при данных функциях спроса и затрат, разделив которую, они смогут извлечь из такого совместного решения большую выгоду, чем из любого другого. Парадокс ситуации, однако, состоит в том, что достичь согласованных действий фирмы не могут, поскольку всякие переговоры между ними запрещены (по условию задачи), а в их отсутствие достичь Парето-эффективного состояния невозможно, поскольку выбор равновесного по Курно выпуска
Докажем, прежде всего, что точка согласованного оптимума не является равновесной по Нэшу. Действительно, оказавшись в точке согласованного оптимума, каждый из игроков может увеличить свою прибыль в одностороннем порядке. Пусть одна из фирм
тогда как прибыль остающейся фирмы – только
Сравнивая, находим, что
Нетрудно увидеть, что Табл.2
Полагая, для примера,
Табл.3
Покажем теперь, что рассмотренная нами форма поведения каждой фирмы может оказаться невыгодной для них в стратегическом плане, если допустить, что конкуренция между фирмами длится неопределенно долго, поскольку в этом случае суммарная дисконтированная прибыль такой фирмы в итоге окажется меньше. Итогом такого рода взаимодействия окажется возможность реализации кооперативного поведения (т.е. достижение эффективного состояния с максимально возможной прибылью). При этом фирмы действуют так, как если бы они заключили друг с другом соглашение, хотя в явном виде такого соглашения не существует.
Пусть
Производить
Суммарный выигрыш
Суммарный выигрыш этой же фирмы от стратегии «нарушение кооперации»:
Фирма предпочтет сотрудничество, если ее выигрыш от кооперации в стратегическом плане окажется больше, нежели от ее нарушения, т.е. если
Это условие эквивалентно следующему неравенству:
или
Подставляя сюда все значения прибылей, находим, что
Распределение
Рассмотрим следующий модельный пример, иллюстрирующий смысл распределительной функции институтов. Допустим, что два человека (А и В) выращивают урожай на общем участке, продают его, и выручку делят пополам. Бомжи «помогают» убирать урожай и, как правило, забирают ровно половину выращенного. Хозяева участка могут нанять охранника, но это стоит денег (издержки производства общественного блага). В игре имеются две стратегии: «нанимать» и «не нанимать». Пусть стоимость всего урожая оценивается в 20 у.е., а стоимость услуг охранника – в 4 у.е. Тогда матрица выигрышей будет иметь вид, соответствующий табл.4. Асимметрия выигрышей налицо, поскольку два равновесия Нэша в игре - (10,6) и (6,10) - отличаются асимметричным распределением выигрышей. Какое из двух реализуется в действительности, - зависит от распределения переговорной силы сторон.
Пусть распределение переговорной силы таково, что
Табл.4. Платежная матрица игры, иллюстрирующей распределительную функцию институтов
Рассмотрим теперь ту же ситуацию в общем виде. Пусть
в противном случае (при выборе стратегии II=«не нанимать»)
Если
Таким образом, в данном случае институт вырастает из доверия людей друг другу (слабого к сильному, народа к государству и, наоборот). В противном случае, когда каждый игрок будет обманываться в своих ожиданиях, институт как способ разрешения конфликта не возникнет. Напротив, возникнет институт тотального недоверия людей друг к другу, причем, если игра будет повторяться, тогда ситуация будет только ухудшаться, поскольку игра пойдет в направлении постоянного уменьшения величины
Другой пример: две фирмы хотят перейти на единый технологический стандарт, который позволит им выпускать совместимую продукцию (табл. 5). Производство по разным стандартам приносит фирмам нулевую прибыль, поэтому они обе заинтересованы в установлении любого из двух равновесий. Но фирма 1 предпочла бы закрепление стандарта 1, ибо тогда она получит бόльшую, чем фирма 2, прибыль. А фирма 2 по той же причине предпочла бы закрепление стандарта 2.
Табл. 5. Игра «выбор технологического стандарта»
Среди институтов, которые решают проблемы дележа и распределения, особый интерес представляют аукционы (торги). Обычно они проводятся по четким, заранее оговоренным правилам, обязательным для всех участников, являя тем самым редкий пример взаимодействий в рамках намеренно создаваемых правил. От этого, в конечном счете, зависит эффективность аукционов (здесь можно привести пример аукциона Викри).
Обеспечив принятие конкретного решения по координации деятельности участников отношений в условиях несимметричного распределения выигрышей, институт тем самым закрепляет неравенство или равенство между ними. Заметим, что лишь в редких случаях участникам отношений безразлично, какое именно равновесие установится в координационной игре. Обычно их предпочтения на этот счет различны. Так, при банкротстве предприятия разные группы его кредиторов заинтересованы в установлении разного приоритета выплат.
Таким образом, некоторые институты ставят одних игроков в более выгодное положение по сравнению с другими. В силу этого в обществе возникает группа, которая стремится такой институт сохранить, и группа, которая стремится его реформировать. Кто победит в этой борьбе, определяется не только и не столько эффективностью данного института, сколько переговорной силой противоборствующих сторон, т.е. распределением власти между группами.
|

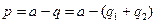 (1)
(1) , предельные издержки каждой фирмы постоянны и равны
, предельные издержки каждой фирмы постоянны и равны  , постоянные издержки отсутствуют, и
, постоянные издержки отсутствуют, и  . В рамках статического подхода, когда фирмы выбирают значение выпуска независимо друг от друга, они оказываются в равновесии Курно-Нэша, где каждая из фирм производит выпуск
. В рамках статического подхода, когда фирмы выбирают значение выпуска независимо друг от друга, они оказываются в равновесии Курно-Нэша, где каждая из фирм производит выпуск (2)
(2)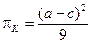 (3)
(3) , (4)
, (4) >
>  (5)
(5) оказывается в этом случае доминирующей стратегией для каждой из фирм. Такой расклад типичен для ситуаций, которые описываются широко известной «дилеммой заключенных».
оказывается в этом случае доминирующей стратегией для каждой из фирм. Такой расклад типичен для ситуаций, которые описываются широко известной «дилеммой заключенных». , выполняя условия сговора, производит
, выполняя условия сговора, производит  в каждом периоде, и продолжает это делать в текущем периоде. Покажем теперь, что если другая (
в каждом периоде, и продолжает это делать в текущем периоде. Покажем теперь, что если другая ( - я) фирма в текущем периоде выберет выпуск, отвечающий равновесию Курно
- я) фирма в текущем периоде выберет выпуск, отвечающий равновесию Курно  (т.е. отклонится от согласованной стратегии), тогда она окажется в выигрыше. Действительно, прибыль уклониста при этом оказывается равной:
(т.е. отклонится от согласованной стратегии), тогда она окажется в выигрыше. Действительно, прибыль уклониста при этом оказывается равной: (6)
(6)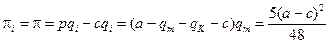 (7)
(7) . Выпишем теперь все полученные прибыли:
. Выпишем теперь все полученные прибыли: и
и  (8)
(8) , так как
, так как  . Все это соответствует раскладу выигрышей в игре «дилемма заключенных», нормальная форма которой имеет вид, приведенный в табл.2:
. Все это соответствует раскладу выигрышей в игре «дилемма заключенных», нормальная форма которой имеет вид, приведенный в табл.2: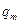 )
)
 ;
;  ;
; 
 ;
; 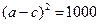 , получим платежную матрицу, соответствующую табл.3. Видно, что каждая из фирм, оказываясь в состоянии «кооперация - кооперация», может увеличить свою прибыль, отклонившись в одностороннем порядке от этой стратегии, т.е. имеет стимул нарушить сговор, что и утверждалось.
, получим платежную матрицу, соответствующую табл.3. Видно, что каждая из фирм, оказываясь в состоянии «кооперация - кооперация», может увеличить свою прибыль, отклонившись в одностороннем порядке от этой стратегии, т.е. имеет стимул нарушить сговор, что и утверждалось. - дисконтный фактор (вероятность продолжения сотрудничества или сговора дуополистов). Рассчитаем значение этого фактора, при котором существует совершенное в подыграх равновесие Курно для бесконечно продолжающейся игры, в которой игроки придерживаются следующей стратегии «спускового курка»:
- дисконтный фактор (вероятность продолжения сотрудничества или сговора дуополистов). Рассчитаем значение этого фактора, при котором существует совершенное в подыграх равновесие Курно для бесконечно продолжающейся игры, в которой игроки придерживаются следующей стратегии «спускового курка»: в первом периоде. В периоде
в первом периоде. В периоде  производить
производить  предшествующих периодов; в противном случае производить выпуск Курно
предшествующих периодов; в противном случае производить выпуск Курно 
 (9)
(9)
 (10)
(10) (11)
(11) (12)
(12)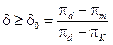 (13)
(13) . Это означает, что если вероятность сотрудничества превышает некое пороговое значение
. Это означает, что если вероятность сотрудничества превышает некое пороговое значение 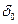 , которое в нашем случае оказывается равным 50%, тогда фирмы будут придерживаться кооперативной стратегии в своих отношениях. На большинстве рынков ситуация, аналогичная игре «дилемма…», как правило, продолжается неопределенно долго. В результате в некоторых отраслях, особенно в тех, где конкурируют только несколько фирм на протяжении длительного времени в условиях стабильного спроса и стабильных издержек, преобладает сотрудничество, даже если при этом не заключаются никакие соглашения договорного порядка. Однако во многих отраслях этого нет. Причин тому несколько. Зачастую это связано с очень большим количеством фирм. В этом случае труднее верить партнерам. Увеличение числа фирм всегда провоцирует определенную нестабильность и усиливает неопределенность. Более же часто провал института сотрудничества является результатом быстрого изменения параметров спроса и издержек.
, которое в нашем случае оказывается равным 50%, тогда фирмы будут придерживаться кооперативной стратегии в своих отношениях. На большинстве рынков ситуация, аналогичная игре «дилемма…», как правило, продолжается неопределенно долго. В результате в некоторых отраслях, особенно в тех, где конкурируют только несколько фирм на протяжении длительного времени в условиях стабильного спроса и стабильных издержек, преобладает сотрудничество, даже если при этом не заключаются никакие соглашения договорного порядка. Однако во многих отраслях этого нет. Причин тому несколько. Зачастую это связано с очень большим количеством фирм. В этом случае труднее верить партнерам. Увеличение числа фирм всегда провоцирует определенную нестабильность и усиливает неопределенность. Более же часто провал института сотрудничества является результатом быстрого изменения параметров спроса и издержек. – сильный, а
– сильный, а  – слабый, и
– слабый, и  )
)
 )
)
 он ему не верит (выше были рассмотрены предельные случае тотальной веры -
он ему не верит (выше были рассмотрены предельные случае тотальной веры - 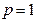 , и тотального неверия -
, и тотального неверия -  - игрока
- игрока 
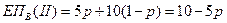
 , и, следовательно,
, и, следовательно,  , тогда
, тогда 


