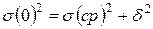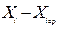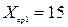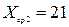Оценка влияния различных факторов на проблему.
Если СС разбита на группы по какому-либо признаку, то для оценки влияния различных факторов, определяющих колеблемость индивидуальных значений признака, можно воспользоваться разложением дисперсии на составляющие: на межгрупповую и внутригрупповую дисперсии. Если рассчитать дисперсию по всей СС, т.е. общую дисперсию Если поставить задачу - выделить в составе общей дисперсии ту ее часть, которая обусловлена влиянием какого-то определенного фактора, то следует разбить СС на группы, положив в основу группировки интересующий нас фактор. Затем надо изучить раздельно вариацию признака внутри однородных в отношении данного фактора групп и изменения в величине признака от группы к группе. Такая группировка позволяет разложить общую дисперсию признака на две дисперсии: 1) дисперсия, характеризующая часть вариации, обусловленную влиянием фактора, лежащего в основе группировки; 2) дисперсия, характеризующая часть вариации, происходящую под влиянием прочих факторов. Отклонение индивидуальных значений признака
Метод дисперсионного анализа (ДА) был разработан Р.А.Фишером около 70 лет тому назад для решения вопросов, связанных с оценкой результатов сельскохозяйственного эксперимента. Метод позволяет количественно определить значимость и долю влияния различных факторов на результативный признак. Метод предполагает анализ небольших серий индивидуальных наблюдений, требует четкого планирования и организации эксперимента и весьма кропотливых расчетов. ДА позволяет: измерять силу влияний, определять их достоверность, оценивать разности частных средних, изучать действие на конечный результат нескольких факторов вместе, роль каждого из них и сравнивать действие отдельных факторов между собой. Основная идея ДА заключается в следующем. Если предположить, что исследуется действие нескольких факторов (Ф1, Ф2, Фj, …Фn) на определенный признак (Х) и что каждый фактор наблюдается m раз, то будет получено n*m наблюдаемых значений. При этом возможно из общей дисперсии Метод ДА может быть использован для изучения влияния различного числа факторов при одинаковом или неодинаковом числе наблюдений в отношении действия каждого из факторов. В связи с этим различают: однофакторный, двухфакторный и многофакторный (3 и более) дисперсионный анализ, а также равномерный и неравномерный комплексы. Основные понятия ДА. В ДА принимаются следующие обозначения и названия. Факторами принято называть любые воздействия или состояния, определяющие ту или иную величину наблюдаемого признака. Обозначаются они обычно заглавными буквами латинского алфавита – А,В,С и т.д. Наблюдаемые признаки, которые испытывают влияние изучаемых факторов, называются результативными Из многих факторов, влияющих на результативный признак, учету подлежит лишь небольшая группа основных, организованных в данном исследовании факторов Из отдельных дат a) равномерные – с одинаковым числом дат в каждой клетке комбинационной таблицы; b) пропорциональные, в которых число дат в различных клетках комбинационной таблицы различно, но соблюдена единая для всего СК пропорциональность между ними; c) непропорциональные, в которых распределение дат по клеткам таблицы различно. Вариация изучаемого признака зависит как от организованных, так и от случайных факторов. Поэтому общая дисперсия
Когда измеряется влияние нескольких факторов (в многофакторном комплексе – группировочной таблице), сумма дисперсий каждого из учитываемых факторов и случайной дисперсии должна быть равна общей дисперсии:
Доля участия отдельных факторов в формировании результативного признака определяется из отношения групповых дисперсий к общей (в процентах). Вычислив отношение факториальной дисперсии
Точно так же вычисляется доля участия случайных факторов
При этом
Межгрупповая дисперсия (влияние группировочного фактора):
Внутригрупповая дисперсия
Между общей дисперсией
Этот метод соответствует положениям теории Адольфа Кетле: Массовые явления в исследуемой совокупности (ИС) формируются под влиянием 2-х групп причин: 1) определяющие состояние массового процесса, связаны с сущностью ИС, формируют типичный уровень для единиц качественно-однородной совокупности 2) индивидуальные случайные причины, не связанные с природой ИС, формируют специфические особенности отдельных единиц ИС Рассмотрим пример влияния фактора обучения на производительность труда (ед.продукции / ед.времени):
|

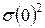 , то она будет характеризовать вариацию признака как результат влияния всех факторов, определяющих индивидуальные различия единиц СС.
, то она будет характеризовать вариацию признака как результат влияния всех факторов, определяющих индивидуальные различия единиц СС.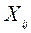 от общей средней
от общей средней 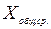 :
: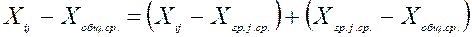
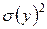 всех наблюдаемых значений выделить дисперсию, являющуюся следствием влияния изучаемых факторов
всех наблюдаемых значений выделить дисперсию, являющуюся следствием влияния изучаемых факторов 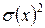 и дисперсию, являющуюся следствием влияния случайных причин, так называемую остаточную дисперсию –
и дисперсию, являющуюся следствием влияния случайных причин, так называемую остаточную дисперсию – 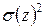 . Сравнивая
. Сравнивая 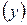 . Отдельные же значения результативного признака именуются датами, вариантами
. Отдельные же значения результативного признака именуются датами, вариантами 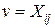 .
.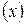 . Учет влияния остальных (неконтролируемых) факторов ведется суммарно, не дифференцированно. Эти факторы называют случайными
. Учет влияния остальных (неконтролируемых) факторов ведется суммарно, не дифференцированно. Эти факторы называют случайными  .
.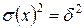 и дисперсии, вызванной случайными факторами – остаточной дисперсии –
и дисперсии, вызванной случайными факторами – остаточной дисперсии – 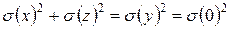
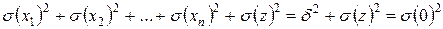
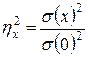
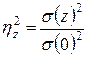
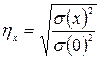 – не что иное, как корреляционное отношение, обычный показатель криволинейной связи двух признаков.
– не что иное, как корреляционное отношение, обычный показатель криволинейной связи двух признаков.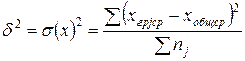 , где nj – число единиц в j –й группе.
, где nj – число единиц в j –й группе.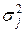 характеризующая вариацию под влиянием прочих случайных факторов:
характеризующая вариацию под влиянием прочих случайных факторов: , а по совокупности в целом вариация значений признака под влиянием прочих факторов характеризуется средней из внутригрупповых дисперсий:
, а по совокупности в целом вариация значений признака под влиянием прочих факторов характеризуется средней из внутригрупповых дисперсий: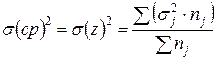
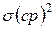 и межгрупповой
и межгрупповой 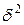 существует соотношение (правило сложения дисперсий):
существует соотношение (правило сложения дисперсий):