Коэффициент детерминации и эмпирическое корреляционное отношение
На основании правил сложения дисперсий можно определить ПОКАЗАТЕЛЬ ТЕСНОТЫ СВЯЗИ между группировочными (признак-фактор) и результативными признаками. Этот показатель называется эмпирическим корреляционным отношением и представляет собой выражение:
Этот показатель говорит о том, что взаимосвязь между фактором и производительностью имеет тесноту связи, то есть вариация данной производительности обусловлена обучением на 86%, а всё остальное - стажем, возрастом, другими случайными факторами. Таким образом, факт профессионального обучения очень желателен. Оценка значимости рассчитанного корреляционного отношения с помощью дисперсионного отношения (F-критерия Фишера, статистики Фишера) F-критерий Фишера применяют для сравнения дисперсий двух выборочных совокупностей. Вычисление ведется по формуле
где
В таблицах F-распределения указываются предельные значения F-критерия для различных комбинаций числа степеней свободы n’1 и n’2, которые могут быть превзойдены с вероятностью 0,05 или 0,01 в силу случайных обстоятельств. Числа степеней свободы для поиска критического значения по таблице F-распределения следует взять равными (n1-1) и (n2-1).
«Таблица пограничных значений показателей достоверности (Fтабл) при Р=0,95 (верхняя строка) и Р=0,99 (нижняя строка)»
Если расчетное значение F-критерия при пятипроцентном уровне значимости и числе степеней свободы к1 и к2 больше табличного, то это позволяет с вероятностью 95% утверждать существенность различий в величине дисперсий и соответственно делать вывод о существенности корреляционной связи между анализируемыми показателями.
Практически все наблюдения выборочные. Поэтому для определения достоверности влияния факторов в группах, в общем случае с разным числом дат – (результатов наблюдений), применяется так называемая девиата, т.е. дисперсия, приходящаяся на один элемент свободного варьирования или на одну степень свободы:
При вычислении общей девиаты имеем
Для факториальной девиаты
Для случайной девиаты
где Корень квадратный из девиаты ( Существенность (достоверность) действия фактора определяется отношением факториальной и случайной девиат:
Это отношение сравнивается со стандартной, табличной величиной «Фишера». Если После выявления причинно-следственных связей между событиями и результатами важно определить зависимость или корреляцию между событиями и временную задержку между ними.
Линейная и временная связь стохастических переменных После выявления причинно-следственных связей между событиями и результатами важно определить зависимость или корреляцию между событиями и временную задержку между ними. Напомним методику. Корреляция. Для выявления степени корреляции между n парами данных для переменных
где
Числитель в правой части выражения для r называется ковариацией. По диаграмме рассеяния, называемой еще полем корреляции, проще всего определить силу связи между случайными величинами
Коэффициент корреляции всегда принимает значение в интервале Однако, если нет корреляции, это не означает, что между Excel позволяет использовать 80 статистических функций (вычисление средних значений, сумм, распределений и стандартных отклонений). Расчет временного лага. Сведем в таблицу число жалоб населения в МЖРЭП на неисправную сантехнику (ед.) и затраты из бюджета МСУ на ремонт сантехники (тыс.руб.) по месяцам 1999 года:
При использовании функции = CORREL(а1,а2) получим коэффициент
Ясно, что наивысшая корреляция достигается при временном лаге в 2 месяца. Но при этом возникает проблема определения суммы затрат
для n пар данных:
При определении линейной зависимости между
Так получена формула (1), которая при использовании в ней коэффициента корреляции r приобретает вид:
Если по данным таблицы вычислить Например, значение
по формуле линии регрессии получим:
тогда при В Excel функция LINEST (ЛИНЕЙН) вычисляет параметры линейного тренда, а функция SLOPE (НАКЛОН) – возвращает наклон линии регрессии. Линию регрессии можно использовать эффективно, когда высок коэффициент корреляции, если Расчет вектора коэффициентов множественной линейной регрессии Линейная модель множественной регрессии имеет вид:
где i – индекс наблюдения. Коэффициент регрессии aj показывает, на какую величину в среднем изменится результативный признак y, если переменную xj увеличить на единицу измерения. Анализ уравнения (1) и методика определения параметров становятся более наглядными, а расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи уравнения (1):
где y — вектор-столбец зависимой переменной размерности n ×1, представляющий собой n наблюдений значений yj; X — матрица n наблюдений независимых переменных x 1, x 2, x 3,..., xm, размерность матрицы X равна n ×(m +1); a — подлежащий оцениванию вектор неизвестных параметров размерности (m +1) ×1; e — вектор случайных отклонений (возмущений) размерности n ×1. Таким образом,
Уравнение (1) содержит значения неизвестных параметров a0, a1, a2,..., am. Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Формула расчета вектора коэффициентов регрессии в векторно-матричной записи имеет вид: а = (ХТХ)-1XTY. (2)
|


 ,
, - значение оценки большей дисперсии
- значение оценки большей дисперсии - значение оценки меньшей дисперсии
- значение оценки меньшей дисперсии , где n’ – число степеней свободы.
, где n’ – число степеней свободы.


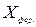 и
и  - частная (групповая, вычисляемая по групповым средним) и общая средние.
- частная (групповая, вычисляемая по групповым средним) и общая средние. ) – известный показатель математической статистики – среднее квадратическое отклонение (s).
) – известный показатель математической статистики – среднее квадратическое отклонение (s).
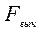 . равно или превышает табличное, то действие изучаемого фактора можно считать доказанным. Когда рассматриваемые факторы существенно влияют на результативный признак, дисперсионный анализ позволяет также измерить и оценить роль различных их градаций и сочетаний.
. равно или превышает табличное, то действие изучаемого фактора можно считать доказанным. Когда рассматриваемые факторы существенно влияют на результативный признак, дисперсионный анализ позволяет также измерить и оценить роль различных их градаций и сочетаний. и
и  ,
,  ,
,  ,…,
,…,  эти данные наносятся на график (диаграмму рассеяния) и для них вычисляется коэффициент корреляции по следующей формуле:
эти данные наносятся на график (диаграмму рассеяния) и для них вычисляется коэффициент корреляции по следующей формуле:
 представляют собой соответственно стандартные отклонения
представляют собой соответственно стандартные отклонения  ,
, 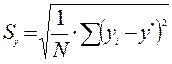
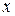 и
и 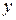 . Ее вид, показывающий тенденцию к росту
. Ее вид, показывающий тенденцию к росту 
 .Если взлеты и падения
.Если взлеты и падения  и
и  y
y 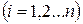 полностью совпадают, то
полностью совпадают, то  , а с ослаблением совпадений
, а с ослаблением совпадений  уменьшается.
уменьшается. – это довольно высокая корреляция. А что получится, если это соответствие сдвинуть? Если, например, имеет место смещение на 1 месяц, т.е.
– это довольно высокая корреляция. А что получится, если это соответствие сдвинуть? Если, например, имеет место смещение на 1 месяц, т.е.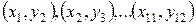 , то поле корреляции будет более выраженным:
, то поле корреляции будет более выраженным:
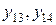 . Для решения задачи используют линию регрессии и формулу ее описывающую:
. Для решения задачи используют линию регрессии и формулу ее описывающую: (1)
(1) ,…,
,…, 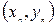 .
. находят значения
находят значения  и
и  методом минимизации суммы квадратов разностей:
методом минимизации суммы квадратов разностей:
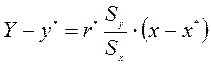
 ,
, 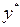 ,
,  ,
,  ,
,  расходов в тыс. руб. в тринадцатом месяце при временном лаге 2 месяца:
расходов в тыс. руб. в тринадцатом месяце при временном лаге 2 месяца: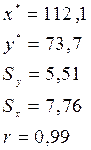

 ,
, 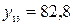
 , то эти рассуждения не имеют смысла.
, то эти рассуждения не имеют смысла. (1)
(1) ,
, ,
,  ,
, 



