Дальнейшие расчеты приведем только для иллюстрации применяемых методов.
(выполнять только на повышенную оценку)
а) Рассчитаем плотность графа G, т.е. наибольшее число вершин подграфа графа G, между всеми вершинами которого задано отношение смежности. Получим матрицы смежности ||H|| и достижимости ||Q|| графа G (рисунок 12).
Рисунок 12 - Матрицы ||H|| и ||Q|| графа G В матрице | | Q|| сформируем блоки, используя метод визуального анализа и перестановок строк (т.е. стоки меняются местами) и перестановок столбцов (т.е. столбцы меняются местами). В итоге получим матрицу ||Q|| на рисунке 13.
Рисунок 13 - Матрица || Q || с тремя выделенными блоками
Анализ матрицы || Q || на рисунке 13 показывает, что поскольку число блоков равно трем, то имеем три полных подграфа G с тремя вершинами в каждом (1-ый блок: 3х3, 2-ой блок: 3х3, 3-ий блок: 2х2). Иными словами, |Х`1|=3, |Х`2|=3, |Х`3|=2 (рисунок 14).
Рисунок 14 - Три подграфа графа G Обозначения: пунктиром выделены полные подграфы графа G.
Таким образом, имеем:
б) Другой алгоритм определения плотности графа приведен в монографии В.А. Горбатова «Фундаментальные основы дискретной математики» на странице 188. Алгоритм приведен в приложении 3.
|
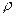(G) графа G 
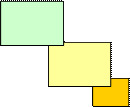8
.
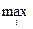
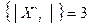