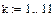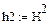Рассмотрим плотность графа G, т.е. наибольшее число вершин пустого подграфа графа G между всеми вершинами которого нет отношений смежности.
Построим обратный граф ┐ G для графа G. Для этого получим матрицу || H || и обратную ей матрицу || ┐ H || (рисунок 15).
Рисунок 15 - Матрицы смежности (слева-направо) графа G и графа ┐ G
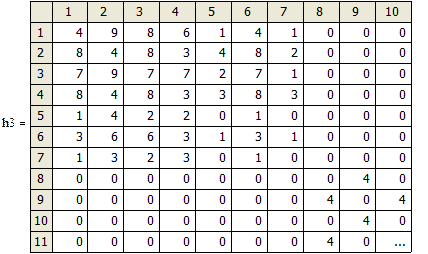
Строим матрицу достижимости графа ┐ G и выполняем операцию перестановки строк и столбцов. Результаты показаны на рисунке 16.

Рисунок 16 - Матрицы достижимости ┐ Qp графа ┐ G
Примечание: матрица на рисунке справа имеет блочную структуру.
На рисунке 17 показан обратный граф ┐ G.
Рисунок 17 - Обратный граф ┐ G
Анализ матрицы ┐ Qp с блочной структурой на рисунке 16 показывает, что поскольку число блоков – три, то имеем три пустых подграфа графа G с тремя вершинами в каждом (рисунок 17):
|Х`1|=3, |Х`2|=3, |Х`3|=3.
Рисунок 18 - Три пустых подграфа графа
G
Таким образом имеем:


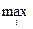
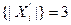 .
.
На этом расчеты числовых характеристик графа G закончены.
| Приложение 1. Построение матрицы достижимости.
|
| Построим матрицу смежности и
зададим единичную матрицу
|
| Возводим в соответствующую
степень
|
| Анализ матриц показывает, что никаких изменений нет. Матрица достижимости:
|


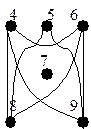



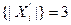 .
.